#include "libmmgcommon_private.h"

Include dependency graph for libmmgs_private.h:

This graph shows which files directly or indirectly include this file:

Macros
#define	MMGS_ALPHAD 3.464101615137755 /* 6.0 / sqrt(3.0) */

#define	MMGS_LOPTL 1.4

#define	MMGS_LOPTS 0.71

#define	MMGS_LLONG 2.0

#define	MMGS_LSHRT 0.3

#define	MMGS_BADKAL 2.e-2

#define	MMGS_NULKAL 1.e-4

#define	MMGS_NPMAX 500000

#define	MMGS_NTMAX 1000000

#define	MMGS_XPMAX 500000

#define	MS_SIN(tag) ((tag & MG_CRN) \|\| (tag & MG_REQ) \|\| (tag & MG_NOM))

#define	MMGS_RETURN_AND_FREE(mesh, met, ls, val)

#define	MMGS_POINT_REALLOC(mesh, sol, ip, wantedGap, law, o, tag)

#define	MMGS_TRIA_REALLOC(mesh, jel, wantedGap, law)

Functions
int	MMGS_Init_mesh_var (va_list argptr)

int	MMGS_Free_all_var (va_list argptr)

int	MMGS_Free_structures_var (va_list argptr)

int	MMGS_Free_names_var (va_list argptr)

int	MMGS_zaldy (MMG5_pMesh mesh)

int	MMGS_assignEdge (MMG5_pMesh mesh)

int	MMGS_analys_for_norver (MMG5_pMesh mesh)

int	MMGS_analys (MMG5_pMesh mesh)

int	MMGS_regver (MMG5_pMesh mesh)

int	MMGS_inqua (MMG5_pMesh, MMG5_pSol)

int	MMGS_outqua (MMG5_pMesh, MMG5_pSol)

int	MMGS_hashTria (MMG5_pMesh)

int	MMGS_setadj (MMG5_pMesh mesh)

int	curvpo (MMG5_pMesh, MMG5_pSol)

int	MMG5_mmgs1 (MMG5_pMesh, MMG5_pSol, MMG5_int *)

int	MMGS_mmgs2 (MMG5_pMesh, MMG5_pSol, MMG5_pSol)

int	MMGS_bdryUpdate (MMG5_pMesh mesh)

int	boulechknm (MMG5_pMesh mesh, MMG5_int start, int ip, MMG5_int *list)

int	bouletrid (MMG5_pMesh mesh, MMG5_int start, MMG5_int ip, int il1, MMG5_int l1, int il2, MMG5_int l2, MMG5_int ip0, MMG5_int ip1)

MMG5_int	MMGS_newPt (MMG5_pMesh mesh, double c[3], double n[3])

void	MMGS_delPt (MMG5_pMesh mesh, MMG5_int ip)

MMG5_int	MMGS_newElt (MMG5_pMesh mesh)

int	MMGS_delElt (MMG5_pMesh mesh, MMG5_int iel)

int	chkedg (MMG5_pMesh, MMG5_int)

int	MMG5_mmgsBezierCP (MMG5_pMesh, MMG5_Tria *, MMG5_pBezier, int8_t ori)

int	MMGS_bezierInt (MMG5_pBezier, double , double , double , double )

int	MMGS_simbulgept (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int ip)

int	MMGS_split1_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int *vx)

int	MMG5_split2_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)

int	MMGS_split3_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)

int	MMGS_split1 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int *vx)

int	MMGS_split2 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)

int	MMGS_split3 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)

int	split1b (MMG5_pMesh mesh, MMG5_int k, int8_t i, MMG5_int ip)

int	chkcol (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i, MMG5_int list, int8_t typchk, double(MMGS_lenEdg)(MMG5_pMesh, MMG5_pSol, MMG5_int, MMG5_int, int8_t), double(*MMGS_caltri)(MMG5_pMesh, MMG5_pSol, MMG5_pTria))

int	colver (MMG5_pMesh mesh, MMG5_int *list, int ilist)

int	colver3 (MMG5_pMesh mesh, MMG5_int *list)

int	colver2 (MMG5_pMesh mesh, MMG5_int *ilist)

int	swapar (MMG5_pMesh mesh, MMG5_int k, int i)

int	chkswp (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, int8_t typchk, double(MMGS_lenEdg)(MMG5_pMesh, MMG5_pSol, MMG5_int, MMG5_int, int8_t), double(MMGS_caltri)(MMG5_pMesh, MMG5_pSol, MMG5_pTria))

int	swpedg (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *list, int ilist, int8_t typchk)

int8_t	typelt (MMG5_pPoint p[3], int8_t *ia)

int	litswp (MMG5_pMesh mesh, MMG5_int k, int8_t i, double kal)

int	litcol (MMG5_pMesh mesh, MMG5_int k, int8_t i, double kal)

int	MMG5_mmgsChkmsh (MMG5_pMesh, int, MMG5_int)

int	paratmet (double c0[3], double n0[3], double m[6], double c1[3], double n1[3], double mt[6])

int	intregmet (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i, double s, double mr[6])

int	MMG5_intridmet (MMG5_pMesh, MMG5_pSol, MMG5_int, MMG5_int, double, double , double )

int	setref (MMG5_pMesh, MMG5_int, MMG5_int, int)

int	delref (MMG5_pMesh)

int	chkmet (MMG5_pMesh, MMG5_pSol)

int	chknor (MMG5_pMesh)

size_t	MMG5_memSize (void)

int	MMGS_memOption (MMG5_pMesh mesh)

int	MMGS_setMeshSize_alloc (MMG5_pMesh mesh)

int	MMG5_mmgsRenumbering (int, MMG5_pMesh, MMG5_pSol, MMG5_pSol, MMG5_int *)

void	MMGS_keep_only1Subdomain (MMG5_pMesh mesh, MMG5_int nsd)

MMG5_int	MMGS_indElt (MMG5_pMesh mesh, MMG5_int kel)

MMG5_int	MMGS_indPt (MMG5_pMesh mesh, MMG5_int kp)

double	caleltsig_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int iel)

double	caleltsig_iso (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int iel)

int	MMGS_defsiz_iso (MMG5_pMesh mesh, MMG5_pSol met)

int	MMGS_defsiz_ani (MMG5_pMesh mesh, MMG5_pSol met)

int	MMGS_doSol_iso (MMG5_pMesh, MMG5_pSol)

int	MMGS_doSol_ani (MMG5_pMesh, MMG5_pSol)

int	MMGS_gradsiz_ani (MMG5_pMesh mesh, MMG5_pSol met)

int	MMGS_gradsizreq_ani (MMG5_pMesh mesh, MMG5_pSol met)

int	intmet_iso (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i, MMG5_int ip, double s)

int	intmet_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i, MMG5_int ip, double s)

int	MMGS_intmet33_ani (MMG5_pMesh, MMG5_pSol, MMG5_int, int8_t, MMG5_int, double)

int	MMGS_paramDisp (MMG5_pMesh, MMG5_int, int8_t, MMG5_int, MMG5_int, double, double[3])

int	MMGS_moveTowardPoint (MMG5_pMesh mesh, MMG5_pPoint p0, MMG5_pPoint p, double llold, double lam0, double lam1, double lam2, double nn1[3], double nn2[3], double to[3])

int	movridpt_iso (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *list, int ilist)

int	movintpt_iso (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *list, int ilist)

int	movridpt_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *list, int ilist)

int	movintpt_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *list, int ilist)

int	MMGS_surfballRotation (MMG5_pMesh, MMG5_pPoint, MMG5_int , int, double r[3][3], double , double n[3])

int	MMGS_prilen (MMG5_pMesh mesh, MMG5_pSol met, int)

int	MMGS_set_metricAtPointsOnReqEdges (MMG5_pMesh, MMG5_pSol, int8_t)

Macro Definition Documentation

◆ MMGS_ALPHAD

#define MMGS_ALPHAD 3.464101615137755 /* 6.0 / sqrt(3.0) */

Definition at line 34 of file libmmgs_private.h.

◆ MMGS_BADKAL

#define MMGS_BADKAL 2.e-2

Definition at line 41 of file libmmgs_private.h.

◆ MMGS_LLONG

#define MMGS_LLONG 2.0

Definition at line 38 of file libmmgs_private.h.

◆ MMGS_LOPTL

#define MMGS_LOPTL 1.4

Definition at line 36 of file libmmgs_private.h.

◆ MMGS_LOPTS

#define MMGS_LOPTS 0.71

Definition at line 37 of file libmmgs_private.h.

◆ MMGS_LSHRT

#define MMGS_LSHRT 0.3

Definition at line 39 of file libmmgs_private.h.

◆ MMGS_NPMAX

#define MMGS_NPMAX 500000

Definition at line 44 of file libmmgs_private.h.

◆ MMGS_NTMAX

#define MMGS_NTMAX 1000000

Definition at line 45 of file libmmgs_private.h.

◆ MMGS_NULKAL

#define MMGS_NULKAL 1.e-4

Definition at line 42 of file libmmgs_private.h.

◆ MMGS_POINT_REALLOC

#define MMGS_POINT_REALLOC	(	mesh,
		sol,
		ip,
		wantedGap,
		law,
		o,
		tag
	)

Value:

  do        \
  {                                                                     \
    MMG5_int klink;                                                     \
    assert ( mesh && mesh->point );                                     \
    MMG5_TAB_RECALLOC(mesh,mesh->point,mesh->npmax,wantedGap,MMG5_Point, \
                       "larger point table",law);                       \
                                                                        \
    mesh->npnil = mesh->np+1;                                           \
    for (klink=mesh->npnil; klink<mesh->npmax-1; klink++)               \
      mesh->point[klink].tmp  = klink+1;                                \
                                                                        \
    /* solution */                                                      \
    if ( sol->m ) {                                                     \
      MMG5_ADD_MEM(mesh,(sol->size*(mesh->npmax-sol->npmax))*sizeof(double), \
                    "larger solution",law);                             \
      MMG5_SAFE_REALLOC(sol->m,sol->size*(sol->npmax+1),               \
                         sol->size*(mesh->npmax+1),double,              \
                         "larger solution",law);                        \
    }                                                                   \
    sol->npmax = mesh->npmax;                                           \
                                                                        \
    /* We try again to add the point */                                 \
    ip = MMGS_newPt(mesh,o,tag);                                       \
    if ( !ip ) {law;}                                                   \
  }while(0)

Reallocation of point table and sol table and creation of point ip with coordinates o and tag tag

Definition at line 66 of file libmmgs_private.h.

◆ MMGS_RETURN_AND_FREE

#define MMGS_RETURN_AND_FREE	(	mesh,
		met,
		ls,
		val
	)

Value:

  do                     \
  {                                                                 \
    if ( !MMGS_Free_all(MMG5_ARG_start,                             \
                        MMG5_ARG_ppMesh,&mesh,MMG5_ARG_ppMet,&met,  \
                        MMG5_ARG_ppLs,&ls,                          \
                        MMG5_ARG_end) ) {                           \
      return MMG5_LOWFAILURE;                                       \
    }                                                               \
    return val;                                                    \
  }while(0)

Free allocated pointers of mesh and sol structure and return value val

Definition at line 53 of file libmmgs_private.h.

◆ MMGS_TRIA_REALLOC

#define MMGS_TRIA_REALLOC	(	mesh,
		jel,
		wantedGap,
		law
	)

Value:

  do                  \
  {                                                                     \
    MMG5_int klink,oldSiz;                                              \
                                                                        \
    oldSiz = mesh->ntmax;                                               \
                                                                        \
    MMG5_CHK_INT32_OVERFLOW(wantedGap,oldSiz,3,5,law);                  \
                                                                        \
    MMG5_TAB_RECALLOC(mesh,mesh->tria,mesh->ntmax,wantedGap,MMG5_Tria,  \
                       "larger tria table",law);                        \
                                                                        \
    mesh->nenil = mesh->nt+1;                                           \
    for (klink=mesh->nenil; klink<mesh->ntmax-1; klink++)               \
      mesh->tria[klink].v[2]  = klink+1;                                \
                                                                        \
    if ( mesh->adja ) {                                                 \
      /* adja table */                                                  \
      MMG5_ADD_MEM(mesh,3*(mesh->ntmax-oldSiz)*sizeof(MMG5_int),        \
                    "larger adja table",law);                           \
      MMG5_SAFE_RECALLOC(mesh->adja,3*oldSiz+5,3*mesh->ntmax+5,MMG5_int \
                          ,"larger adja table",law);                    \
    }                                                                   \
                                                                        \
    /* We try again to add the point */                                 \
    jel = MMGS_newElt(mesh);                                            \
    if ( !jel ) {law;}                                                  \
  }while(0)

Reallocation of tria table and creation of tria jel

Definition at line 94 of file libmmgs_private.h.

◆ MMGS_XPMAX

#define MMGS_XPMAX 500000

Definition at line 46 of file libmmgs_private.h.

◆ MS_SIN

#define MS_SIN ( tag ) ((tag & MG_CRN) || (tag & MG_REQ) || (tag & MG_NOM))

Definition at line 49 of file libmmgs_private.h.

Function Documentation

◆ boulechknm()

int boulechknm	(	MMG5_pMesh	mesh,
		MMG5_int	start,
		int	ip,
		MMG5_int *	list
	)

Parameters

mesh	pointer to the mesh structure.
start	index of tetra to start to compute the ball.
ip	index of point in tetra start for which we want to compute the ball.
list	pointer to the computed ball of point.

Returns: size of list if success, -size if overflow, 0 if cfg is non-manifold.

Find all triangles sharing ip, \(list[0] = start\) . Do not stop when crossing ridge. Check whether resulting configuration is manifold.

Definition at line 51 of file boulep_s.c.

Here is the caller graph for this function:

◆ bouletrid()

int bouletrid	(	MMG5_pMesh	mesh,
		MMG5_int	start,
		MMG5_int	ip,
		int *	il1,
		MMG5_int *	l1,
		int *	il2,
		MMG5_int *	l2,
		MMG5_int *	ip0,
		MMG5_int *	ip1
	)

Parameters

mesh	pointer to the mesh structure.
start	index of the starting triangle.
ip	index of the looked ridge point.
il1	pointer to the first ball size.
l1	pointer to the first computed ball (associated to n1's side).
il2	pointer to the second ball size.
l2	pointer to the second computed ball (associated to n2's side).
global	ip0 index of the first extremity of the ridge.
global	ip1 index of the second extremity of the ridge.

Returns: 0 if fail, 1 otherwise.

Computation of the two balls of a ridge point: the list l1 is associated to normal n1's side. ip0 and ip1 are the indices of the 2 ending point of the ridge. Both lists are returned enumerated in direct order.

Definition at line 201 of file boulep_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ caleltsig_ani()

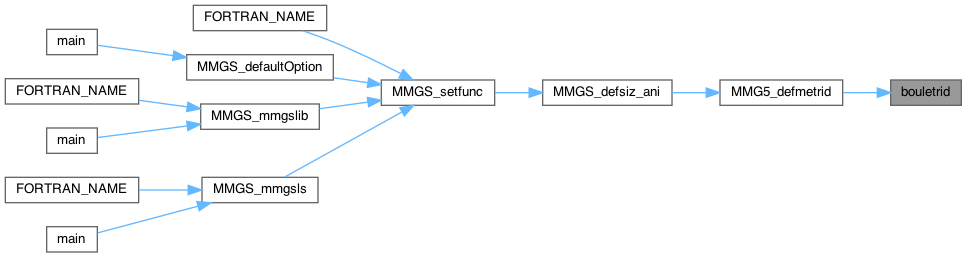
double caleltsig_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	iel
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
iel	element index

Returns: 0 if fail, -1 if orientation is reversed with regards to orientation of vertices, the computed quality otherwise.

Quality function identic to caltri_ani but puts a sign according to deviation to normal to vertices.

Definition at line 54 of file quality_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ caleltsig_iso()

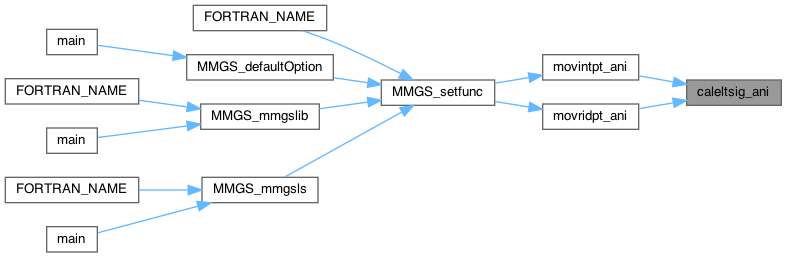
double caleltsig_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	iel
	)

Definition at line 141 of file quality_s.c.

Here is the caller graph for this function:

◆ chkcol()

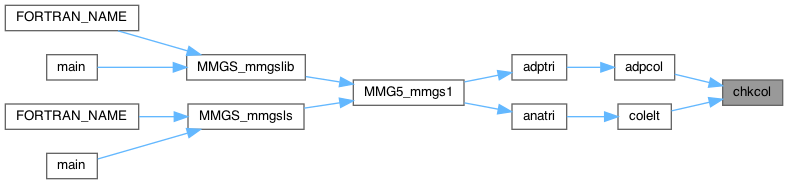
int chkcol	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i,
		MMG5_int *	list,
		int8_t	typchk,
		double(*)(MMG5_pMesh, MMG5_pSol, MMG5_int, MMG5_int, int8_t)	MMGS_lenEdg,
		double(*)(MMG5_pMesh, MMG5_pSol, MMG5_pTria)	MMGS_caltri
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
k	index of the element in wich we collapse
i	index of the edge to collapse
list	pointer to the ball of point
typchk	type of check to perform
MMGS_lenEdg	pointer to the suitable fct to compute edge lengths depending on presence of input metric, metric type (iso/aniso) and typchk value (i.e. stage of adaptation)
MMGS_caltri	pointer to the suitable fct to compute tria quality depending on presence of input metric, metric type (iso/aniso) and typchk value (i.e. stage of adaptation)

Returns: 0 if we can't move of if we fail, 1 if success

check if geometry preserved by collapsing edge i

Definition at line 59 of file colver_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ chkedg()

int chkedg	(	MMG5_pMesh	mesh,
		MMG5_int	iel
	)

Definition at line 214 of file mmgs1.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ chkmet()

int chkmet	(	MMG5_pMesh	,
		MMG5_pSol
	)

◆ chknor()

int chknor ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh

Returns: 1 if success, 0 if fail.

Check normal vectors consistency

Warning: unused

Definition at line 242 of file chkmsh_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ chkswp()

int chkswp	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		int8_t	typchk,
		double(*)(MMG5_pMesh, MMG5_pSol, MMG5_int, MMG5_int, int8_t)	MMGS_lenEdg,
		double(*)(MMG5_pMesh, MMG5_pSol, MMG5_pTria)	MMGS_caltri
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
k	index of the element in wich we perform the edge swap
i	index of the edge to swap
typchk	type of check to perform
MMGS_lenEdg	pointer to the suitable fct to compute edge lengths depending on presence of input metric, metric type (iso/aniso) and typchk value (i.e. stage of adaptation)
MMGS_caltri	pointer to the suitable fct to compute tria quality depending on presence of input metric, metric type (iso/aniso) and typchk value (i.e. stage of adaptation)

Check whether edge i of triangle k should be swapped for geometric approximation purposes

Definition at line 58 of file swapar_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ colver()

int colver	(	MMG5_pMesh	mesh,
		MMG5_int *	list,
		int	ilist
	)

Definition at line 280 of file colver_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ colver2()

int colver2	(	MMG5_pMesh	mesh,
		MMG5_int *	ilist
	)

Definition at line 433 of file colver_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ colver3()

int colver3	(	MMG5_pMesh	mesh,
		MMG5_int *	list
	)

Parameters

mesh	pointer to the mesh structure.
list	pointer to the ball of the point to collapse.

Returns: 1 if success, 0 if fail.

Collapse edge \(list[0]\%3\) in tet \(list[0]/3\) ( \( ip->i1\) ) for a ball of the collapsed point of size 3: the collapsed point is removed.

Definition at line 370 of file colver_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ curvpo()

int curvpo	(	MMG5_pMesh	,
		MMG5_pSol
	)

◆ delref()

int delref ( MMG5_pMesh mesh )

Definition at line 39 of file gentools_s.c.

◆ intmet_ani()

int intmet_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i,
		MMG5_int	ip,
		double	s
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	element index.
i	local index of edge in k.
ip	global index of the new point in which we want to compute the metric.
s	interpolation parameter (between 0 and 1).

Returns: 0 if fail, 1 otherwise.

Interpolation of anisotropic sizemap at parameter s along edge i of elt k for special storage of ridges metrics (after defsiz call).

Definition at line 104 of file intmet_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ intmet_iso()

int intmet_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i,
		MMG5_int	ip,
		double	s
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	triangle in which we interpole the metrics.
i	edge along which we interpole the metrics.
ip	index of point in which we compute the interpolated metric.
s	parameter at which we compute the interpolation.

Returns: 1 if success, 0 otherwise.

Linear interpolation of sizemap along edge i of tria k.

Definition at line 77 of file intmet_s.c.

Here is the caller graph for this function:

◆ intregmet()

int intregmet	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i,
		double	s,
		double	mr[6]
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	element index.
i	local index of edge in k.
s	interpolation parameter.
mr	computed metric.

Returns: call to MMG5_interpreg_ani (thus, 0 if fail, 1 otherwise).

Metric interpolation on edge i in elt it at parameter \( 0 <= s0 <= 1 \) from p1 result is stored in mr. edge \( p_1-p_2 \) must not be a ridge.

Definition at line 57 of file intmet_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ litcol()

int litcol	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int8_t	i,
		double	kal
	)

Definition at line 473 of file colver_s.c.

Here is the call graph for this function:

◆ litswp()

int litswp	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int8_t	i,
		double	kal
	)

◆ MMG5_intridmet()

int MMG5_intridmet	(	MMG5_pMesh	,
		MMG5_pSol	,
		MMG5_int	,
		MMG5_int	,
		double	,
		double *	,
		double *
	)

◆ MMG5_memSize()

size_t MMG5_memSize ( void )

Returns: the available memory size of the computer.

Compute the available memory size of the computer.

Definition at line 852 of file tools.c.

Here is the caller graph for this function:

◆ MMG5_mmgs1()

int MMG5_mmgs1	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	permNodGlob
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
permNodGlob	if provided, strore the global permutation of nodes.

Returns: 0 if failed, 1 if success.

Main adaptation routine.

Definition at line 1462 of file mmgs1.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_mmgsBezierCP()

int MMG5_mmgsBezierCP	(	MMG5_pMesh	mesh,
		MMG5_Tria *	pt,
		MMG5_pBezier	pb,
		int8_t	ori
	)

Parameters

mesh	pointer to the mesh structure.
pt	pointer to the triangle structure.
pb	pointer to the computed Bezier structure.
ori	triangle orientation (unused but here for compatibility with the MMG5_bezierCP interface).

Returns: 1.

Compute Bezier control points on triangle pt (cf. [4]).

Todo:: merge with the MMG5_mmg3dBezierCP function and remove the pointer toward this functions.

Definition at line 54 of file bezier_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_mmgsChkmsh()

int MMG5_mmgsChkmsh	(	MMG5_pMesh	mesh,
		int	severe,
		MMG5_int	base
	)

Parameters

mesh	pointer to the mesh structure.
severe	level of performed check
base	unused argument.

Returns: 0 if fail, 1 if success.

Check the mesh validity

Definition at line 48 of file chkmsh_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_mmgsRenumbering()

int MMG5_mmgsRenumbering	(	int	boxVertNbr,
		MMG5_pMesh	mesh,
		MMG5_pSol	sol,
		MMG5_pSol	fields,
		MMG5_int *	permNodGlob
	)

Parameters

boxVertNbr	number of vertices by box.
mesh	pointer to the mesh structure.
sol	pointer to the solution structure
fields	pointer to an array of solution fields
permNodGlob	array to store the global permutation of nodes (if provided)

Returns: 0 if the renumbering fail and we can't rebuild tetrahedra hashtable, 1 if the renumbering fail but we can rebuild tetrahedra hashtable or if the renumbering success.

Modifies the node indicies to prevent from cache missing.

Definition at line 80 of file librnbg_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_split2_sim()

int MMG5_split2_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns: 0 if split leads to invalid element, else 1.

Simulate the splitting of element k along the 2 edges i1 and i2. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 383 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_analys()

int MMGS_analys ( MMG5_pMesh mesh )

Definition at line 1094 of file analys_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_analys_for_norver()

int MMGS_analys_for_norver ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure.

Returns: 1 if succeed, 0 if fail

Preprocessing stage: mesh analysis.

Definition at line 1042 of file analys_s.c.

Here is the call graph for this function:

◆ MMGS_assignEdge()

int MMGS_assignEdge ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure.

Returns: 1 if success, 0.

Copy the properties (ref and tag) of the declared edges to the triangles, where they are assigned to the individual corners of the triangle. First a hash is created for rapid lookup of the edges. Then in a loop over all edges of all triangles, the hash is probed for each edge, and if it exists its properties are copied. Thus, declared edges that do not occur in any triangle will be silently ignored.

Remarks: this function handle all the provided edges.

Definition at line 113 of file hash_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_bdryUpdate()

int MMGS_bdryUpdate ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure.

Returns: 1 if success, 0.

Copy the edge tags stored in triangles in the other triangles sharing the edge.

Definition at line 169 of file hash_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_bezierInt()

int MMGS_bezierInt	(	MMG5_pBezier	,
		double *	,
		double *	,
		double *	,
		double *
	)

◆ MMGS_defsiz_ani()

int MMGS_defsiz_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric stucture.

Returns: 0 if fail, 1 otherwise.

Define size at points by intersecting the surfacic metric and the physical metric.

The output metric is:

at singular points: isotropic
at ridge points: anisotropic in the orthonormal basis defined by the tangent at the ridge and the normal at each portion of surface.
at surface boundary points: anisotropic in an orthonormal basis difined in the tangent plane and the direction normal to this plane.

Warning: What we are doing on non-manifold points has to be improved: as such points are marked as MG_CRN and MG_REQ, we first try to call MMG5_defmetsin that likely fails (because MMG5_boulet don't work for non-manifod points due to the missing of consistent adjacencies relationships), then we call MMG5_defUninitSize and we set hmax on non-manifold points. Note that the building of adjacency table depends on the initial mesh numbering, thus, in certain cases, MMG5_boulet will succeed...

Step 1: Set metric at points belonging to a required edge: compute the metric as the mean of the length of the required eges passing through the point

Step 2: Travel all the points (via triangles) in the mesh and set metric tensor

search for unintialized metric

Remark: as non manifold points are marked as CRN and REQ, we first try to call defmetsin that fails (because MMG5_boulet don't work for non-manifod points), then we pass here and we set hmax on non-manifold points

Definition at line 735 of file anisosiz_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_defsiz_iso()

int MMGS_defsiz_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns: 1 if success, 0 if fail

Define isotropic size map at all vertices of the mesh, associated with geometric approx ; by convention, p0->h stores desired length at point p0

Step 1: Set metric at points belonging to a required edge: compute the metric as the mean of the length of the required eges passing through the point

Step 2: size at non required internal points

Step 3: Minimum size feature imposed by the hausdorff distance

Definition at line 142 of file isosiz_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_delElt()

int MMGS_delElt	(	MMG5_pMesh	mesh,
		MMG5_int	iel
	)

Parameters

mesh	pointer to the mesh
iel	index of the element to delete

Returns: 1 if success, 0 if fail

Delete the element iel

Definition at line 93 of file zaldy_s.c.

Here is the caller graph for this function:

◆ MMGS_delPt()

void MMGS_delPt	(	MMG5_pMesh	mesh,
		MMG5_int	ip
	)

Definition at line 58 of file zaldy_s.c.

Here is the caller graph for this function:

◆ MMGS_doSol_ani()

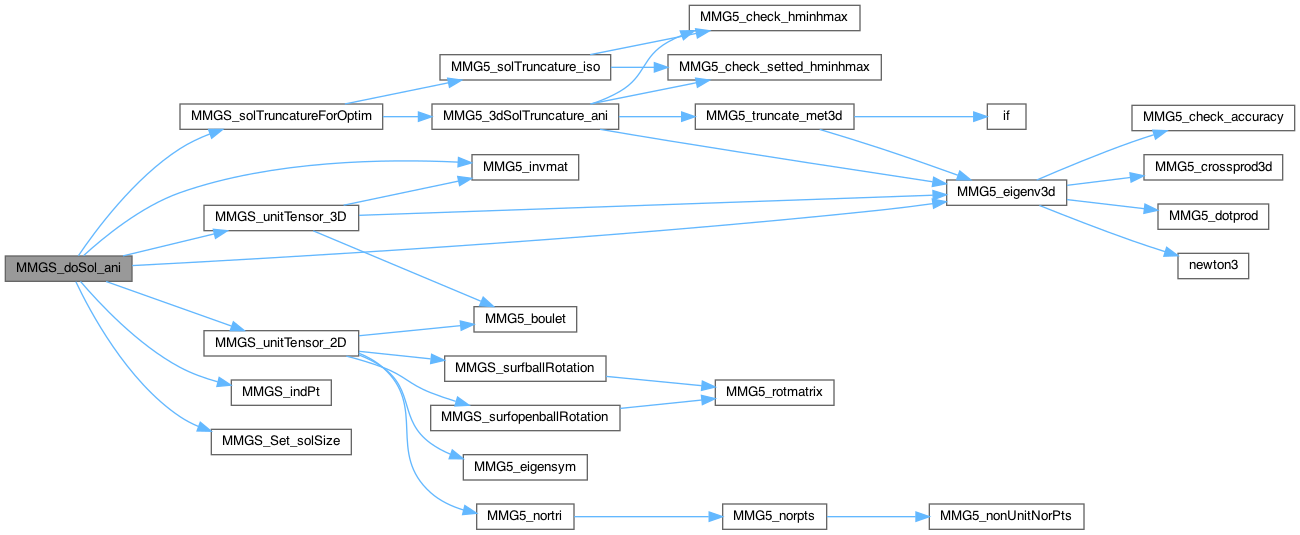
int MMGS_doSol_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns: 1 if succeed, 0 if fail

Remarks: need the normal at vertices.; hmax/hmin may be not setted here so we can't use it.

Compute the unit metric tensor at mesh vertices (from edges passing through the vertices).

Increment base marker to detect points already processed

Step 1: treat non-manifold points: travel triangle edges and add edge contribution to extremities (we have to do that because ball of non-manifold points can't be computed)

Corner point (no normal at vertex): if the corner defines an angle we can compute the 3D unit tensor (non singular), in the other cases (corner along a flat surface, for example because it is at the intersection of 3 specific edges or because it is provided by the user) we will project the edges onto the tangent plane and compute the 2D unit tensor (as for required and regular points)

Required point (no normal at vertex): projection of edges onto the tangent plane and computation of the 2D unit tensor

Ridge point (2 normals): normally we can compute the 3D unit tensor. If the angle is too flat, the computation fails and we try to compute the 2D unit tensor on the tangent plane of the point.

Regular or reference point: projection of edges onto the tangent plane and computation of the 2D unit metric tensor

Step 3: check computed metric

Step 4: computation of hmin/hmax (if needed) and metric truncature

Definition at line 1334 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_doSol_iso()

int MMGS_doSol_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns: 1 if succeed, 0 if fail

Remarks: need the normal at vertices.

Compute isotropic size map according to the mean of the length of the edges passing through a point.

Definition at line 859 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Free_all_var()

int MMGS_Free_all_var ( va_list argptr )

Parameters

argptr list of the mmg structures that must be deallocated. Each structure must follow one of the MMG5_ARG preprocessor variable that allow to identify it.

argptr contains at least a pointer to a MMG5_pMesh structure (that will contain the mesh and identified by the MMG5_ARG_ppMesh keyword).

To call the MMGS_mmgslib function, you must also provide a pointer to a MMG5_pSol structure (that will contain the ouput metric (and the input one, if provided) and identified by the MMG5_ARG_ppMet keyword).

To call the MMGS_mmgsls function, you must also provide a pointer toward a MMG5_pSol structure (that will contain the level-set function and identified by the MMG5_ARG_ppLs keyword).

Returns: 0 if fail, 1 if success

Internal function for deallocations before return (taking a va_list as argument).

Remarks: we pass the structures by reference in order to have argument compatibility between the library call from a Fortran code and a C code.

Definition at line 225 of file variadic_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Free_names_var()

int MMGS_Free_names_var ( va_list argptr )

Parameters

argptr list of the mmg structures for whose we want to deallocate the name. Each structure must follow one of the MMG5_ARG preprocessor variable that allow to identify it.

argptr contains at least a pointer to a MMG5_pMesh structure (that will contain the mesh and identified by the MMG5_ARG_ppMesh keyword).

To call the MMGS_mmgslib function, you must also provide a pointer to a MMG5_pSol structure (that will contain the ouput metric (and the input one, if provided) and identified by the MMG5_ARG_ppMet keyword).

To call the MMGS_mmgsls function, you must also provide a pointer toward a MMG5_pSol structure (that will contain the level-set function and identified by the MMG5_ARG_ppLs keyword).

Returns: 0 if fail, 1 if success

Internal function for name deallocations before return (taking a va_list as argument).

Remarks: we pass the structures by reference in order to have argument compatibility between the library call from a Fortran code and a C code.

Definition at line 426 of file variadic_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Free_structures_var()

int MMGS_Free_structures_var ( va_list argptr )

Parameters

argptr list of the mmg structures that must be deallocated. Each structure must follow one of the MMG5_ARG* preprocessor variable that allow to identify it.

argptr contains at least a pointer to a MMG5_pMesh structure (that will contain the mesh and identified by the MMG5_ARG_ppMesh keyword).

To call the MMGS_mmgslib function, you must also provide a pointer to a MMG5_pSol structure (that will contain the ouput metric (and the input one, if provided) and identified by the MMG5_ARG_ppMet keyword).

To call the MMGS_mmgsls function, you must also provide a pointer toward a MMG5_pSol structure (that will contain the level-set function and identified by the MMG5_ARG_ppLs keyword).

Returns: 0 if fail, 1 if success

Internal function for structures deallocations before return (taking a va_list as argument).

Remarks: we pass the structures by reference in order to have argument compatibility between the library call from a Fortran code and a C code.

Definition at line 324 of file variadic_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_gradsiz_ani()

int MMGS_gradsiz_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.

Returns: 1

Enforces mesh gradation by truncating metric field.

Definition at line 835 of file anisosiz_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_gradsizreq_ani()

int MMGS_gradsizreq_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

◆ MMGS_hashTria()

int MMGS_hashTria ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure.

Returns: 1 if success, 0 if fail.

Create adjacency table.

Definition at line 77 of file hash_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_indElt()

MMG5_int MMGS_indElt	(	MMG5_pMesh	mesh,
		MMG5_int	kel
	)

find the element number in packed numerotation

Definition at line 123 of file gentools_s.c.

Here is the caller graph for this function:

◆ MMGS_indPt()

MMG5_int MMGS_indPt	(	MMG5_pMesh	mesh,
		MMG5_int	kp
	)

find the point number in packed numerotation

Definition at line 139 of file gentools_s.c.

Here is the caller graph for this function:

◆ MMGS_Init_mesh_var()

int MMGS_Init_mesh_var ( va_list argptr )

Parameters

argptr list of the mmg structures that must be initialized. Each structure must follow one of the MMG5_ARG* preprocessor variable that allow to identify it.

argptr contains at least a pointer to a MMG5_pMesh structure (that will contain the mesh and identified by the MMG5_ARG_ppMesh keyword).

To call the MMGS_mmgslib function, you must also provide a pointer to a MMG5_pSol structure (that will contain the ouput metric (and the input one, if provided) and identified by the MMG5_ARG_ppMet keyword).

Returns: 0 if fail, 1 if success

To call the MMGS_mmgsls function, you must also provide a pointer toward a MMG5_pSol structure (that will contain the level-set function and identified by the MMG5_ARG_ppLs keyword).

Internal function for structure allocations (taking a va_list argument).

Definition at line 149 of file variadic_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_inqua()

int MMGS_inqua	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.

Returns: 0 if the worst element has a nul quality, 1 otherwise.

Print histogram of mesh qualities for classical storage of ridges metrics (so before the the MMG5_defsiz function call).

Definition at line 399 of file quality_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_intmet33_ani()

int MMGS_intmet33_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i,
		MMG5_int	ip,
		double	s
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	element index.
i	local index of edge in k.
ip	global index of the new point in which we want to compute the metric.
s	interpolation parameter (between 0 and 1).

Returns: 0 if fail, 1 otherwise.

Interpolation of anisotropic sizemap at parameter s along edge i of elt k for classic storage of ridges metrics (before defsiz call).

Definition at line 144 of file intmet_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_keep_only1Subdomain()

void MMGS_keep_only1Subdomain	(	MMG5_pMesh	mesh,
		MMG5_int	nsd
	)

Parameters

mesh	pointer to the mesh structure.
nsd	index of subdomain to keep.

Keep only subdomain of index nsd and remove other subdomains.

Definition at line 161 of file gentools_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_memOption()

int MMGS_memOption ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure

Returns: 0 if fail, 1 otherwise

memory repartition for the -m option

Definition at line 205 of file zaldy_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_mmgs2()

int MMGS_mmgs2	(	MMG5_pMesh	mesh,
		MMG5_pSol	sol,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
sol	pointer to the level-set
met	pointer to a metric (optionnal)

Returns: 0 if fail, 1 otherwise.

Create implicit surface in mesh.

Definition at line 241 of file mmgs2.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_moveTowardPoint()

int MMGS_moveTowardPoint	(	MMG5_pMesh	mesh,
		MMG5_pPoint	p0,
		MMG5_pPoint	p,
		double	llold,
		double	lam0,
		double	lam1,
		double	lam2,
		double	nn1[3],
		double	nn2[3],
		double	to[3]
	)

Parameters

mesh	pointer to the mesh
p0	point to move.
p	neighbouring point toward which we try to move.
llold	init length of edge p0-p
lam0	first bezier basis function (order 2)
lam1	second bezier basis function (order 2)
lam2	third bezier basis function (order 2)
nn1	normal at point p0 after relocation
nn2	normal at point p0 after relocation
to	tangent along edge at point p0 after relocation

Returns: 1 if success, 0 if fail

Update normals and tangent at ref or ridge point p0 after relocation at coordinates o.

Definition at line 555 of file movpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_newElt()

MMG5_int MMGS_newElt ( MMG5_pMesh mesh )

Definition at line 71 of file zaldy_s.c.

Here is the caller graph for this function:

◆ MMGS_newPt()

MMG5_int MMGS_newPt	(	MMG5_pMesh	mesh,
		double	c[3],
		double	n[3]
	)

Definition at line 39 of file zaldy_s.c.

Here is the caller graph for this function:

◆ MMGS_outqua()

int MMGS_outqua	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.

Returns: 0 if the worst element has a nul quality, 1 otherwise.

Print histogram of mesh qualities for special storage of ridges metrics (after the MMG5_defsiz function call).

Definition at line 467 of file quality_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_paramDisp()

int MMGS_paramDisp	(	MMG5_pMesh	mesh,
		MMG5_int	it,
		int8_t	isrid,
		MMG5_int	ip0,
		MMG5_int	ip,
		double	step,
		double	o[3]
	)

Parameters

mesh	pointer to the mesh
it	triangle to which belongs the edge along which we move
isrid	1 if the edge is a ridge
ip0	edge point that we want to move
ip	edge point connected by the ref/ridge edge to p0
step	displacement factor along the ref/ridge edge
o	coordinates of point after relocation

Returns: 1 if success, 0 otherwise.

Infer arc length of displacement along ref or ridge edge, parameterized over edges.

Definition at line 375 of file movpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_prilen()

int MMGS_prilen	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		int	metRidTyp
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
metRidTyp	Type of storage of ridges metrics: 0 for classic storage, 1 for special storage.

Returns: 0 if fail, 1 otherwise.

Compute sizes of edges of the mesh, and displays histo.

Definition at line 283 of file quality_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_regver()

int MMGS_regver ( MMG5_pMesh mesh )

Parameters

mesh	pointer to a MMG5 mesh structure.

Returns: 0 if fail, 1 otherwise.

Regularization procedure for vertices coordinates, dual Laplacian for a surface mesh.

Definition at line 817 of file analys_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_set_metricAtPointsOnReqEdges()

int MMGS_set_metricAtPointsOnReqEdges	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		int8_t	ismet
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
ismet	1 if user provided metric

Returns: 0 if fail, 1 otherwise

Compute the metric at points on trequired adges as the mean of the lengths of the required eges to which belongs the point. The processeed points are marked with flag 3.

Definition at line 90 of file isosiz_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_setadj()

int MMGS_setadj ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh

Returns: 1 if success, 0 if fail

topology: set adjacent, detect Moebius, flip faces, count connected comp.

Definition at line 47 of file analys_s.c.

Here is the caller graph for this function:

◆ MMGS_setMeshSize_alloc()

int MMGS_setMeshSize_alloc ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh structure.

Returns: 0 if failed, 1 otherwise.

Allocation of the array fields of the mesh.

Definition at line 223 of file zaldy_s.c.

Here is the caller graph for this function:

◆ MMGS_simbulgept()

int MMGS_simbulgept	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int	ip
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of the starting triangle.
i	local index of the edge to split in k.
ip	index of the point that we try to create.

Returns: 0 if final position is invalid or if computation of bezier patch fails, 1 if all checks are ok.

Simulate the creation of the point ip, to be inserted at an edge. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Remarks: Don't work for non-manifold edge.

Definition at line 162 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_split1()

int MMGS_split1	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
i	index of edge to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns: 1 if success, 0 if fail.

Split element k along edge i.

Definition at line 109 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_split1_sim()

int MMGS_split1_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
i	index of edge to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.
k	index of element to split.

Returns: 0 if split leads to invalid element, else 1.

Simulate the splitting of element k along edge i. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 52 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_split2()

int MMGS_split2	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns: 1 if success, 0 if fail.

Split element k along the 2 edges i1 and i2.

Definition at line 459 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_split3()

int MMGS_split3	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns: 1 if success, 0 if fail.

Split element k along the 3 edges

Definition at line 620 of file split_s.c.

Here is the call graph for this function:

◆ MMGS_split3_sim()

int MMGS_split3_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns: 0 if split leads to invalid element, else 1.

Simulate the splitting of element k along the 3 edges. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 532 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_surfballRotation()

int MMGS_surfballRotation	(	MMG5_pMesh	mesh,
		MMG5_pPoint	p0,
		MMG5_int *	list,
		int	ilist,
		double	r[3][3],
		double *	lispoi,
		double	n[3]
	)

Parameters

mesh	pointer to the mesh structure.
p0	starting point
list	ball of p0
ilist	number of tria in the ball of p0
r	rotation that send the normal at p0 onto the z vector
lipoint	rotated ball of point p0
n	normal at point p0

Returns: 1 if success, 0 otherwise.

Compute the rotation matrix that sends the tangent plane at p0 onto z=0 and apply this rotation to the ball of p0.

Definition at line 529 of file anisosiz_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_zaldy()

int MMGS_zaldy ( MMG5_pMesh mesh )

Parameters

mesh	pointer to the mesh

Returns: 1 if success, 0 if fail

allocate main structure

Definition at line 263 of file zaldy_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ movintpt_ani()

int movintpt_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	list,
		int	ilist
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
list	ball of point.
ilist	size of the point ball.

Returns: 0 if fail, 1 otherwise.

Compute movement of an internal point whose ball is passed.

Step 2 : Compute gradient towards optimal position = centre of mass of the ball, projected to tangent plane

Step 3 : locate new point in the ball, and compute its barycentric coordinates

Step 4 : come back to original problem, and compute patch in triangle iel

Definition at line 49 of file anisomovpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ movintpt_iso()

int movintpt_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	list,
		int	ilist
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
list	pointer to the ball of the point.
ilist	size of the ball.

Returns: 0 if we can't move the point, 1 if we can.

Move internal point whose volumic is passed.

Definition at line 52 of file movpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ movridpt_ani()

int movridpt_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	list,
		int	ilist
	)

Definition at line 252 of file anisomovpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ movridpt_iso()

int movridpt_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	list,
		int	ilist
	)

Definition at line 595 of file movpt_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ paratmet()

int paratmet	(	double	c0[3],
		double	n0[3],
		double	m[6],
		double	c1[3],
		double	n1[3],
		double	mt[6]
	)

◆ setref()

int setref	(	MMG5_pMesh	mesh,
		MMG5_int	start,
		MMG5_int	ref,
		int	putreq
	)

Parameters

mesh	pointer to the mesh
start	index of the tetra from which we start
ref	reference to set
putreq	1 if boundary edges must be set to required

Returns: 1 if success, 0 if fail

Start from triangle start, and pile up triangles by adjacency, till a GEO or REF curve is met ; pass all references of travelled faces to ref ; putreq = 1 if boundary edges met must be set to MG_REQ, 0 otherwise.

Definition at line 64 of file gentools_s.c.

◆ split1b()

int split1b	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int8_t	i,
		MMG5_int	ip
	)

Parameters

mesh	pointer to the mesh structure.
k	index of element to split.
i	index of edge to split.
ip	index of the new point.

Returns: 0 if lack of memory, 1 otherwise.

Split element k along edge i, inserting point ip and updating the adjacency relations.

Remarks: do not call this function in non-manifold case

Definition at line 283 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ swapar()

int swapar	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int	i
	)

Parameters

mesh	poiner toward the mesh structure.
k	elt index.
i	index of the elt edge to swap.

Returns: 1

Warning: the quality of the resulting triangles is not checked here... It must be checked outside to prevent the creation of empty elts.

Definition at line 318 of file swapar_s.c.

Here is the caller graph for this function:

◆ swpedg()

int swpedg	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int *	list,
		int	ilist,
		int8_t	typchk
	)

◆ typelt()

int8_t typelt	(	MMG5_pPoint	p[3],
		int8_t *	ia
	)

Definition at line 525 of file quality_s.c.

Macros

Functions

Macro Definition Documentation

◆ MMGS_ALPHAD

◆ MMGS_BADKAL

◆ MMGS_LLONG

◆ MMGS_LOPTL

◆ MMGS_LOPTS

◆ MMGS_LSHRT

◆ MMGS_NPMAX

◆ MMGS_NTMAX

◆ MMGS_NULKAL

◆ MMGS_POINT_REALLOC

◆ MMGS_RETURN_AND_FREE

◆ MMGS_TRIA_REALLOC

◆ MMGS_XPMAX

◆ MS_SIN

Function Documentation

◆ boulechknm()

◆ bouletrid()

◆ caleltsig_ani()

◆ caleltsig_iso()

◆ chkcol()

◆ chkedg()

◆ chkmet()

◆ chknor()

◆ chkswp()

◆ colver()

◆ colver2()

◆ colver3()

◆ curvpo()

◆ delref()

◆ intmet_ani()

◆ intmet_iso()

◆ intregmet()

◆ litcol()

◆ litswp()

◆ MMG5_intridmet()

◆ MMG5_memSize()

◆ MMG5_mmgs1()

◆ MMG5_mmgsBezierCP()

◆ MMG5_mmgsChkmsh()

◆ MMG5_mmgsRenumbering()

◆ MMG5_split2_sim()

◆ MMGS_analys()

◆ MMGS_analys_for_norver()

◆ MMGS_assignEdge()

◆ MMGS_bdryUpdate()

◆ MMGS_bezierInt()

◆ MMGS_defsiz_ani()

◆ MMGS_defsiz_iso()

◆ MMGS_delElt()

◆ MMGS_delPt()

◆ MMGS_doSol_ani()

◆ MMGS_doSol_iso()

◆ MMGS_Free_all_var()

◆ MMGS_Free_names_var()

◆ MMGS_Free_structures_var()

◆ MMGS_gradsiz_ani()

◆ MMGS_gradsizreq_ani()

◆ MMGS_hashTria()

◆ MMGS_indElt()

◆ MMGS_indPt()

◆ MMGS_Init_mesh_var()

◆ MMGS_inqua()

◆ MMGS_intmet33_ani()

◆ MMGS_keep_only1Subdomain()

◆ MMGS_memOption()

◆ MMGS_mmgs2()

◆ MMGS_moveTowardPoint()

◆ MMGS_newElt()

◆ MMGS_newPt()

◆ MMGS_outqua()

◆ MMGS_paramDisp()

◆ MMGS_prilen()

◆ MMGS_regver()

◆ MMGS_set_metricAtPointsOnReqEdges()

◆ MMGS_setadj()

◆ MMGS_setMeshSize_alloc()

◆ MMGS_simbulgept()