Fonctions for anisotropic size map computation. More...

#include "mmgcommon_private.h"
#include "mmgexterns_private.h"
#include "inlined_functions_private.h"

Include dependency graph for anisosiz.c:

Functions
static double	MMG5_surf (MMG5_pMesh mesh, double m[3][6], MMG5_pTria ptt)

double	MMG5_surftri_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_pTria ptt)

double	MMG5_surftri33_ani (MMG5_pMesh mesh, MMG5_pTria ptt, double ma[6], double mb[6], double mc[6])

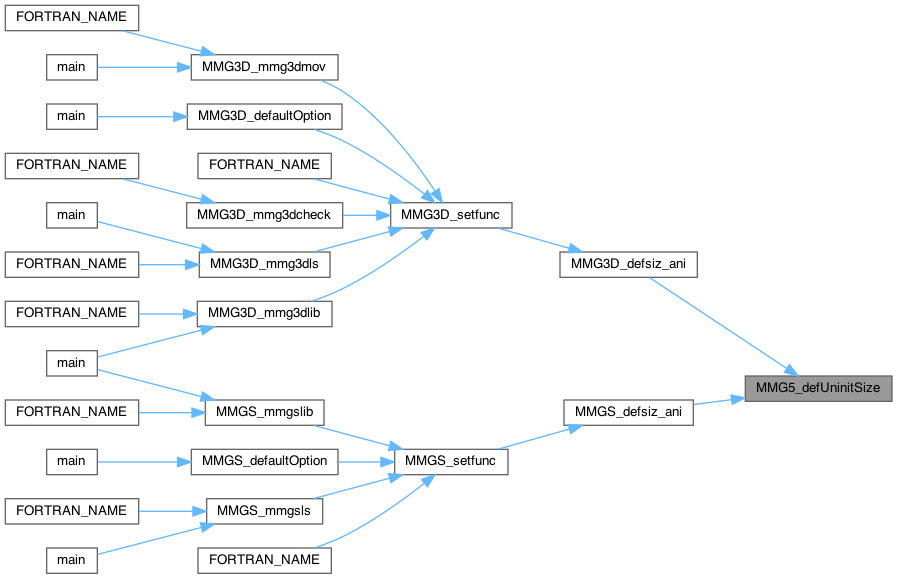
void	MMG5_defUninitSize (MMG5_pMesh mesh, MMG5_pSol met, int8_t ismet)

void	MMG5_fillDefmetregSys (MMG5_int k, MMG5_pPoint p0, int i0, MMG5_Bezier b, double r[3][3], double c[3], double *lispoi, double tAA[6], double tAb[3])

int	MMG5_solveDefmetregSys (MMG5_pMesh mesh, double r[3][3], double c[3], double tAA[6], double tAb[3], double *m, double isqhmin, double isqhmax, double hausd)

int	MMG5_solveDefmetrefSys (MMG5_pMesh mesh, MMG5_pPoint p0, MMG5_int ipref[2], double r[3][3], double c[3], double tAA[6], double tAb[3], double *m, double isqhmin, double isqhmax, double hausd)

double	MMG5_ridSizeInTangentDir (MMG5_pMesh mesh, MMG5_pPoint p0, MMG5_int idp, MMG5_int *iprid, double isqhmin, double isqhmax)

double	MMG5_ridSizeInNormalDir (MMG5_pMesh mesh, int i0, double bcu, MMG5_Bezier b, double isqhmin, double isqhmax)

MMG5_int	MMG5_grad2metSurf (MMG5_pMesh mesh, MMG5_pSol met, MMG5_pTria pt, MMG5_int np1, MMG5_int np2)

int	MMG5_simred2d (MMG5_pMesh mesh, double m, double n, double dm[2], double dn[2], double vp[2][2])

int	MMG5_simred3d (MMG5_pMesh mesh, double m, double n, double dm[3], double dn[3], double vp[3][3])

void	MMG5_sort_simred (int8_t dim, double dm, double dn, double vp, double swap, int8_t *perm)

int	MMG5_test_simred2d (MMG5_pMesh mesh, double mex, double nex, double dmex, double dnex, double vpex[][2])

int	MMG5_test_simred3d (MMG5_pMesh mesh, double mex, double nex, double dmex, double dnex, double vpex[][3])

int	MMG5_updatemet2d_ani (double m, double n, double dm[2], double dn[2], double vp[2][2], int8_t ier)

int	MMG5_updatemet3d_ani (double m, double n, double dm[3], double dn[3], double vp[3][3], int8_t ier)

int	MMG5_test_updatemet2d_ani ()

int	MMG5_test_updatemet3d_ani ()

void	MMG5_gradEigenvreq (double dm, double dn, double difsiz, int8_t dir, int8_t *ier)

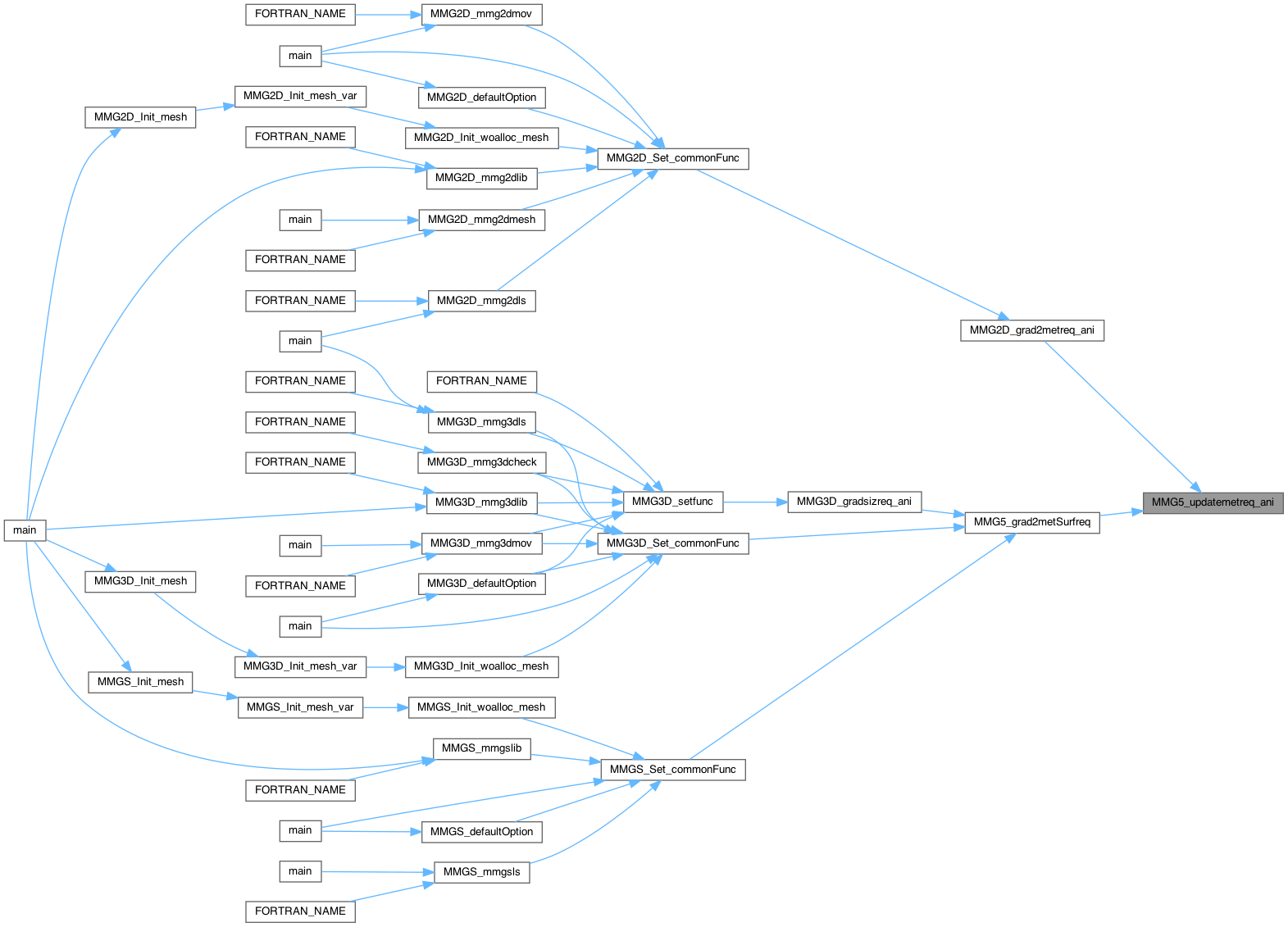
int	MMG5_updatemetreq_ani (double *n, double dn[2], double vp[2][2])

int	MMG5_grad2metSurfreq (MMG5_pMesh mesh, MMG5_pSol met, MMG5_pTria pt, MMG5_int npmaster, MMG5_int npslave)

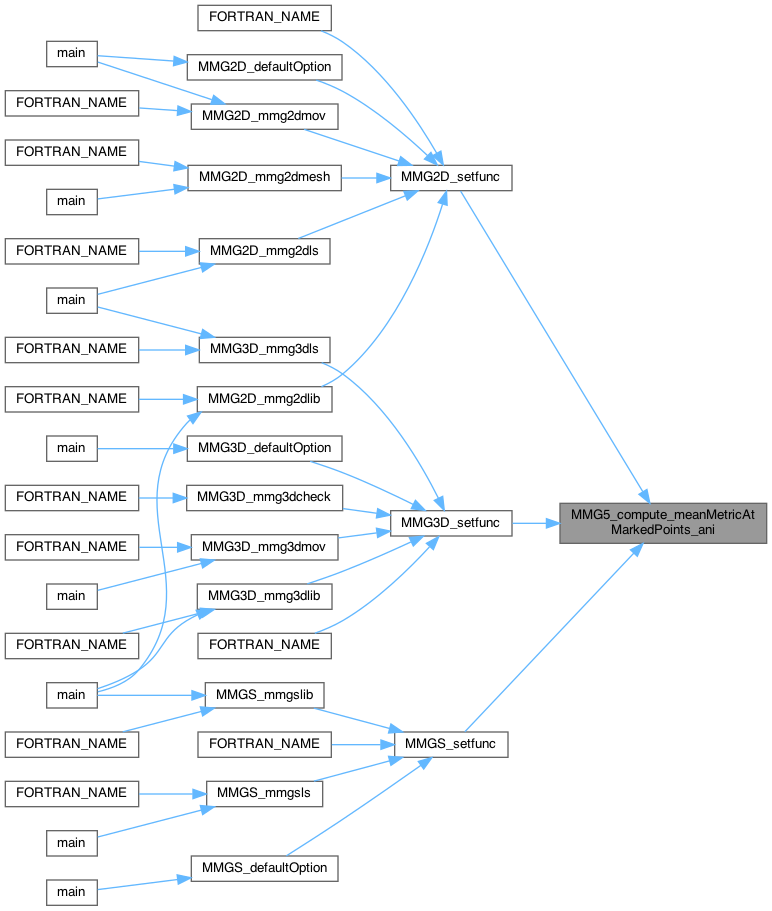
int	MMG5_compute_meanMetricAtMarkedPoints_ani (MMG5_pMesh mesh, MMG5_pSol met)

MMG5_int	MMG5_gradsiz_ani (MMG5_pMesh mesh, MMG5_pSol met, int *it)

int	MMG5_gradsizreq_ani (MMG5_pMesh mesh, MMG5_pSol met)

Detailed Description

Fonctions for anisotropic size map computation.

Author: Charles Dapogny (UPMC); Cécile Dobrzynski (Bx INP/Inria/UBordeaux); Pascal Frey (UPMC); Algiane Froehly (Inria/UBordeaux)

Version: 5

Copyright: GNU Lesser General Public License.

Definition in file anisosiz.c.

Function Documentation

◆ MMG5_compute_meanMetricAtMarkedPoints_ani()

int MMG5_compute_meanMetricAtMarkedPoints_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.

Returns: 1 if success, 0 if fail.

Compute the mean metric at mesh points with a non-nul s field. At the beginning, for a given point ip, $ met->m[met->size * ip] $ contains the sum of n metrics and the s field of ip contains the number of metrics summed in the point. Set the flag of the processed points to 3.

Definition at line 2205 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_defUninitSize()

void MMG5_defUninitSize	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		int8_t	ismet
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
ismet	1 if user provided metric.

Search for points with unintialized metric and define anisotropic size at this points.

Definition at line 228 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_fillDefmetregSys()

void MMG5_fillDefmetregSys	(	MMG5_int	k,
		MMG5_pPoint	p0,
		int	i0,
		MMG5_Bezier	b,
		double	r[3][3],
		double	c[3],
		double *	lispoi,
		double	tAA[6],
		double	tAb[3]
	)

Parameters

k	index of the tetrahedra from which we come.
p0	pointer to the point on which we want to def the metric.
i0	pointer to the local index of the point in tria.
b	control polygon of triangle.
r	rotation matrix.
c	physical coordinates of the curve edge mid-point.
lispoi	list of incident vertices to p0
tAA	matrix to fill
tAb	second member

Fill matrice \sum tAA and second member \sum tAb with $ A=( X_{P_i}^2 Y_{P_i}^2 X_{P_i}Y_{P_i}) $ and $ b= Z_{P_i}$ with P_i the physical points at edge [i0;i1] extremities and middle. Compute the physical coor c of the curve edge's mid-point for a regular or reference point.

Definition at line 290 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_grad2metSurf()

MMG5_int MMG5_grad2metSurf	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pTria	pt,
		MMG5_int	np1,
		MMG5_int	np2
	)

Parameters

mesh	pointer to the mesh.
met	pointer to the metric structure.
pt	pointer to a triangle.
np1	global index of the first extremity of the edge.
np2	global index of the second extremity of the edge.

Returns: -1 if no gradation is needed, else index of graded point.

Enforces gradation of metric in one extremity of edge $f[ np1; np2]$f in tria pt with respect to the other, along the direction of the associated support curve first, then along the normal direction.

Warning: The gradation along the direction normal to the surface is made in an "isotropic way".

Remarks: ALGIANE: a mettre à plat : dans le cas d'une métrique très aniso avec la grande taille quasiment dans la direction de l'arête on se retrouve à modifier la grande taille uniquement (car proche de l'arête) sauf que cette modification n'a quasi pas d'influence sur le calcul de la longueur d'arête.

Definition at line 975 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_grad2metSurfreq()

int MMG5_grad2metSurfreq	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pTria	pt,
		MMG5_int	npmaster,
		MMG5_int	npslave
	)

Parameters

mesh	pointer to the mesh.
met	pointer to the metric structure.
pt	pointer to the processed triangle.
npmaster	edge extremity that cannot be modified
npslave	edge extremity to modify to respect the gradation.

Returns: 0 if no gradation is needed, 1 otherwise.

Enforces gradation of metric of the extremity ±a npslave of edge $f[ npmaster; npslave]$f in tria pt with respect to the other, along the direction of the associated support curve first, then along the normal direction.

Warning: The gradation along the direction normal to the surface is made in an "isotropic way".

Definition at line 1951 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_gradEigenvreq()

void MMG5_gradEigenvreq	(	double *	dm,
		double *	dn,
		double	difsiz,
		int8_t	dir,
		int8_t *	ier
	)

Parameters

dm	eigenvalues of the first matrix (not modified)
dn	eigenvalues of the second matrix (modified)
difsiz	maximal size gap authorized by the gradation.
dir	direction in which the sizes are graded.
ier	2 if dn has been updated, 0 otherwise.

Gradation of size dn = 1/sqrt(eigenv of the tensor) for required points in the idir direction.

Definition at line 1883 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_gradsiz_ani()

MMG5_int MMG5_gradsiz_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		int *	it
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
it	number of performed iteration (to fill)

Returns: nup, the number of points updated.

Standard gradation procedure.

Mark the edges belonging to a required entity

Definition at line 2259 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_gradsizreq_ani()

int MMG5_gradsizreq_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.

Returns: 1

Enforces mesh gradation (on required entities) by truncating metric field.

Mark the edges belonging to a required entity (already done if the classic gradation is enabled)

Definition at line 2322 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_ridSizeInNormalDir()

double MMG5_ridSizeInNormalDir	(	MMG5_pMesh	mesh,
		int	i0,
		double *	bcu,
		MMG5_Bezier *	b,
		double	isqhmin,
		double	isqhmax
	)

Parameters

mesh	pointer to the mesh structure.
i0	local index in the face of the point on which we want to compute the metric
bcu	pointer to the barycentric coordinates of vector u in the looked face.
b	bezier control polygon for the looked face.
isqhmin	minimum edge size.
isqhmax	maximum edge size.

Returns: the computed ridge size in first or second normal direction (depending of i0).

Compute the specific size of a ridge in the direction of the normal of the looked face. This wanted size is computed as using the majoration of the haudorff distance between a triangle and its ideal curve approximation by the Hessian of the signed distance function to the ideal surface. See documentation of MMG5_ridSizeInTangentDir function.

Definition at line 836 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_ridSizeInTangentDir()

double MMG5_ridSizeInTangentDir	(	MMG5_pMesh	mesh,
		MMG5_pPoint	p0,
		MMG5_int	idp,
		MMG5_int *	iprid,
		double	isqhmin,
		double	isqhmax
	)

Parameters

mesh	pointer to the mesh structure.
p0	pointer to the point at which we define the metric.
idp	global index of the point at which we define the metric.
iprid	pointer to the two extremities of the ridge.
isqhmin	minimum edge size.
isqhmax	maximum edge size.

Returns: the computed ridge size in the tangent direction.

Compute the specific size that we want to apply to a ridge in the direction of the tangent of the ridge. This wanted size is computed as using the majoration of the haudorff distance between a triangle and its ideal curve approximation by the Hessian of the signed distance function to the ideal surface.

\[ d^H(\partial \Omega,S_T) \leq \displaystyle\frac{1}{2}\left( \frac{d-1}{d} \right)^2 \max\limits_{T\in S_T} \max\limits_{x \in T } \max\limits_{y,z \in T} \langle \left| H(d_\omega)(x) \right| yz,yz\rangle. \]

where $ d^H(\partial \Omega,S_T) $ is the distance between the triangle $S_T$ and the ideal boundary (reconstructed using cubic Bezier patches) $ \partial \Omega $, $ d$ is the mesh dimension and $ H(d_\Omega) $ is the hessian matrix of the signed distance function to $ \Omega $.

For all $ x \in \partial \Omega $, $H(d_\omega)(x)$ is the second fundamental form whose eigenvalues are the principal curvatures ( $\kappa_1 $ and $ \kappa_2 $) of $ \partial \Omega $ at $ x $ so the previous formula can be rewritten as:

\[ d^H(\partial \Omega,S_T) \leq \displaystyle\frac{1}{2}\left( \frac{d-1}{d} \right)^2 \max( \left|\kappa_1\right|,\left|\kappa_2\right|). \]

As we want to respect the imposed the hausd threshold and we are interessed to get the wanted size along the tangent direction at the ridge point only, finally, m is computed as

\[ m = \kappa \frac{1}{2\textrm{hausd}} \left(\frac{d-1}{d} \right)^2. \]

See Theorem 1 of [3].

Definition at line 764 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_simred2d()

int MMG5_simred2d	(	MMG5_pMesh	mesh,
		double *	m,
		double *	n,
		double	dm[2],
		double	dn[2],
		double	vp[2][2]
	)

Parameters

mesh	pointer to the mesh
m	first matrix
n	second matrix
dm	eigenvalues of m in the coreduction basis (to fill)
dn	eigenvalues of n in the coreduction basis (to fill)
vp	coreduction basis (to fill)

Returns: 0 if fail 1 otherwise.

Perform simultaneous reduction of matrices m and n.

Definition at line 1326 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_simred3d()

int MMG5_simred3d	(	MMG5_pMesh	mesh,
		double *	m,
		double *	n,
		double	dm[3],
		double	dn[3],
		double	vp[3][3]
	)

Parameters

mesh	pointer to the mesh
m	first matrix
n	second matrix
dm	eigenvalues of m in the coreduction basis (to fill)
dn	eigenvalues of n in the coreduction basis (to fill)
vp	coreduction basis (to fill)

Returns: 0 if fail 1 otherwise.

Perform simultaneous reduction of matrices m and n.

Definition at line 1416 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_solveDefmetrefSys()

int MMG5_solveDefmetrefSys	(	MMG5_pMesh	mesh,
		MMG5_pPoint	p0,
		MMG5_int	ipref[2],
		double	r[3][3],
		double	c[3],
		double	tAA[6],
		double	tAb[3],
		double *	m,
		double	isqhmin,
		double	isqhmax,
		double	hausd
	)

Parameters

mesh	pointer to the mesh structure.
p0	pointer to the point on which we want to define the metric.
ipref	table containing the indices of the edge extremities.
r	pointer to the rotation matrix.
c	physical coordinates of the curve edge mid-point.
tAA	matrix of the system to solve.
tAb	second member.
m	pointer to the metric.
isqhmax	maximum size for edge.
isqhmin	minimum size for edge.
hausd	hausdorff value at point (unused).

Returns: 1 if success, 0 if fail.

Solve tAA * tmp_m = tAb and fill m with tmp_m (after rotation) for a ref point.

Definition at line 538 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_solveDefmetregSys()

int MMG5_solveDefmetregSys	(	MMG5_pMesh	mesh,
		double	r[3][3],
		double	c[3],
		double	tAA[6],
		double	tAb[3],
		double *	m,
		double	isqhmin,
		double	isqhmax,
		double	hausd
	)

Parameters

mesh	pointer to the mesh structure.
r	pointer to the rotation matrix.
c	physical coordinates of the curve edge mid-point.
tAA	matrix of the system to solve.
tAb	second member.
m	pointer to the metric.
isqhmax	maximum size for edge.
isqhmin	minimum size for edge.
hausd	hausdorff value at point.

Returns: 1 if success, 0 if fail.

Solve tAA * tmp_m = tAb and fill m with tmp_m (after rotation) for a regular point.

Definition at line 436 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_sort_simred()

void MMG5_sort_simred	(	int8_t	dim,
		double *	dm,
		double *	dn,
		double *	vp,
		double *	swap,
		int8_t *	perm
	)

Parameters

dim	square matrix size
dm	diagonal values array
dn	diagonal values array
vp	basis vectors array
swap	swap array
perm	permutation array

Sort and permute diagonal values (and basis vectors) in increasing order with respect to the first matrix.

Definition at line 1562 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_surf()

static double MMG5_surf	(	MMG5_pMesh	mesh,
		double	m[3][6],
		MMG5_pTria	ptt
	)

inlinestatic

Parameters

mesh	pointer to the mesh structure.
m	pointer to the metric at triangle vertices.
ptt	pointer to the triangle structure.

Returns: The double of the triangle area.

Compute the double of the area of the surface triangle ptt with respect to the anisotropic metric m.

Definition at line 50 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_surftri33_ani()

double MMG5_surftri33_ani	(	MMG5_pMesh	mesh,
		MMG5_pTria	ptt,
		double	ma[6],
		double	mb[6],
		double	mc[6]
	)

Parameters

mesh	pointer to the mesh structure.
ptt	pointer to the triangle structure.
ma	metric at triangle vertex.
mb	metric at triangle vertex.
mc	metric at triangle vertex.

Returns: The double of the triangle area.

Compute the double of the area of the surface triangle ptt with respect to the anisotropic metric met (for classic storage of ridges metrics).

Definition at line 171 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_surftri_ani()

double MMG5_surftri_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pTria	ptt
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
ptt	pointer to the triangle structure.

Returns: The double of the triangle area.

Compute the double of the area of the surface triangle ptt with respect to the anisotropic metric met (for special storage of ridges metrics).

Definition at line 124 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_test_simred2d()

int MMG5_test_simred2d	(	MMG5_pMesh	mesh,
		double *	mex,
		double *	nex,
		double *	dmex,
		double *	dnex,
		double	vpex[][2]
	)

Parameters

mesh	pointer to the mesh structure
mex	first symmetric test matrix
nex	second symmetric test matrix
dm	diagonalization of the first matrix on the reduction basis
dn	diagonalization of the second matrix on the reduction basis
vp	simultaneous reduction basis (stored by columns)

Returns: 1 if success, 0 if fail

For a couple of 2x2 symmetric matrices, Test:

the computation of the simultaneous reduction values of the matrices;
the computation of the simultaneous reduction basis vectors..

Compute simultaneous reduction

Recompose matrices from diagonal values

Definition at line 1585 of file anisosiz.c.

Here is the call graph for this function:

◆ MMG5_test_simred3d()

int MMG5_test_simred3d	(	MMG5_pMesh	mesh,
		double *	mex,
		double *	nex,
		double *	dmex,
		double *	dnex,
		double	vpex[][3]
	)

Parameters

mesh	pointer to the mesh structure
mex	first symmetric test matrix
nex	second symmetric test matrix
dm	diagonalization of the first matrix on the reduction basis
dn	diagonalization of the second matrix on the reduction basis
vp	simultaneous reduction basis (stored by columns)

Returns: 1 if success, 0 if fail

For a couple of 3x3 symmetric matrices, Test:

the computation of the simultaneous reduction values of the matrices;
the computation of the simultaneous reduction basis vectors..

Compute simultaneous reduction

Recompose matrices from diagonal values

Definition at line 1663 of file anisosiz.c.

Here is the call graph for this function:

◆ MMG5_test_updatemet2d_ani()

int MMG5_test_updatemet2d_ani ( )

Test Update of the metrics = tP^-1 diag(d0,d1)P^-1, P = (vp[0], vp[1]) stored in columns in 2D.

Recompose matrices from exact simultaneous diagonalization

Definition at line 1805 of file anisosiz.c.

Here is the call graph for this function:

◆ MMG5_test_updatemet3d_ani()

int MMG5_test_updatemet3d_ani ( )

Test Update of the metrics = tP^-1 diag(d0,d1)P^-1, P = (vp[0], vp[1]) stored in columns in 3D.

Recompose matrices from exact simultaneous diagonalization

Definition at line 1841 of file anisosiz.c.

Here is the call graph for this function:

◆ MMG5_updatemet2d_ani()

int MMG5_updatemet2d_ani	(	double *	m,
		double *	n,
		double	dm[2],
		double	dn[2],
		double	vp[2][2],
		int8_t	ier
	)

inline

Parameters

m	first matrix
n	second matrix
dm	eigenvalues of m in the coreduction basis
dn	eigenvalues of n in the coreduction basis
vp	coreduction basis
ier	flag of the updated sizes: (ier & 1) if we dm has been modified, (ier & 2) if dn has been modified.

Returns: 0 if fail, 1 otherwise

Update of the metrics = tP^-1 diag(d0,d1)P^-1, P = (vp[0], vp[1]) stored in columns in 2D.

Definition at line 1742 of file anisosiz.c.

Here is the caller graph for this function:

◆ MMG5_updatemet3d_ani()

int MMG5_updatemet3d_ani	(	double *	m,
		double *	n,
		double	dm[3],
		double	dn[3],
		double	vp[3][3],
		int8_t	ier
	)

inline

Parameters

m	first matrix
n	second matrix
dm	eigenvalues of m in the coreduction basis
dn	eigenvalues of n in the coreduction basis
vp	coreduction basis
ier	flag of the updated sizes: (ier & 1) if we dm has been modified, (ier & 2) if dn has been modified.

Returns: 0 if fail, 1 otherwise

Update of the metrics = tP^-1 diag(d0,d1)P^-1, P = (vp[0], vp[1]) stored in columns in 3D.

Definition at line 1783 of file anisosiz.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMG5_updatemetreq_ani()

int MMG5_updatemetreq_ani	(	double *	n,
		double	dn[2],
		double	vp[2][2]
	)

Parameters

n	matrix to update
dn	eigenvalues of n in the coreduction basis
vp	coreduction basis

Returns: 0 if fail, 1 otherwise

Update of the metric n = tP^-1 diag(dn0,dn1)P^-1, P = (vp[0], vp[1]) stored in columns

Definition at line 1914 of file anisosiz.c.

Here is the caller graph for this function:

Functions

Detailed Description

Function Documentation

◆ MMG5_compute_meanMetricAtMarkedPoints_ani()

◆ MMG5_defUninitSize()

◆ MMG5_fillDefmetregSys()

◆ MMG5_grad2metSurf()

◆ MMG5_grad2metSurfreq()

◆ MMG5_gradEigenvreq()

◆ MMG5_gradsiz_ani()

◆ MMG5_gradsizreq_ani()

◆ MMG5_ridSizeInNormalDir()

◆ MMG5_ridSizeInTangentDir()

◆ MMG5_simred2d()

◆ MMG5_simred3d()

◆ MMG5_solveDefmetrefSys()

◆ MMG5_solveDefmetregSys()

◆ MMG5_sort_simred()

◆ MMG5_surf()

◆ MMG5_surftri33_ani()

◆ MMG5_surftri_ani()

◆ MMG5_test_simred2d()

◆ MMG5_test_simred3d()

◆ MMG5_test_updatemet2d_ani()

◆ MMG5_test_updatemet3d_ani()

◆ MMG5_updatemet2d_ani()

◆ MMG5_updatemet3d_ani()

◆ MMG5_updatemetreq_ani()