 |
Mmg
Simplicial remeshers (mesh adaptation, isovalue discretization, lagrangian movement)
|
 |
Mmg
Simplicial remeshers (mesh adaptation, isovalue discretization, lagrangian movement)
|
Functions to create new points. More...
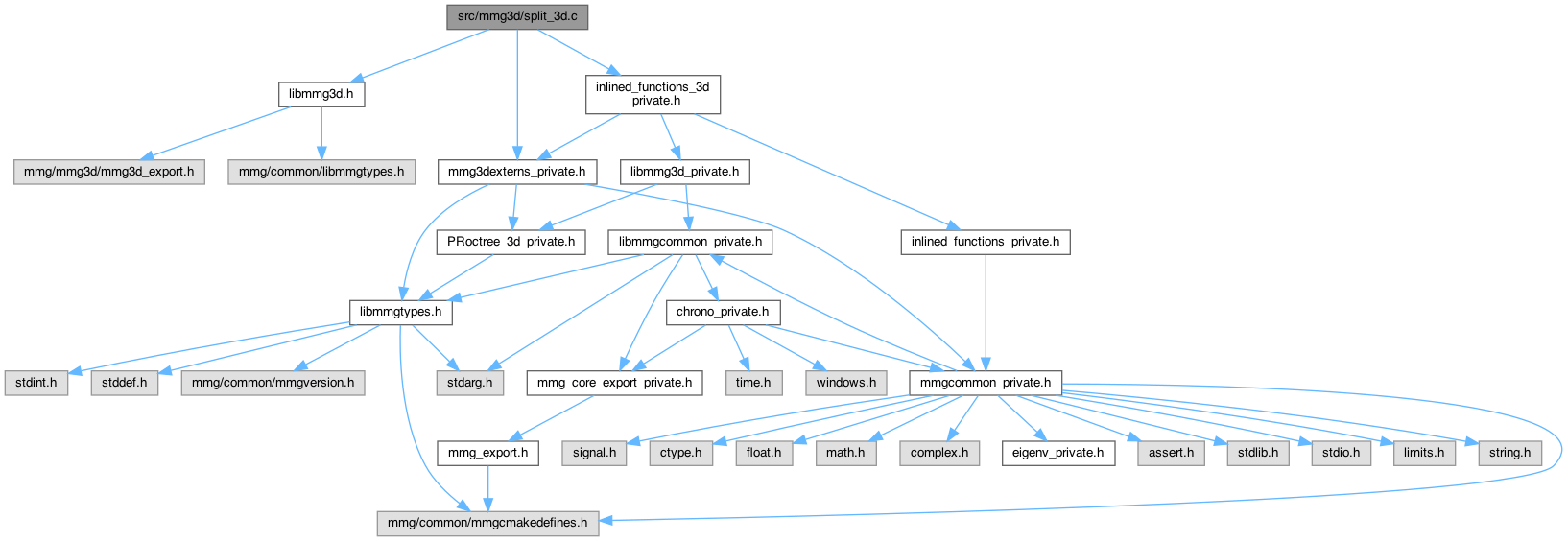
Go to the source code of this file.
Functions | |
| void | MMG3D_split1_cfg (MMG5_int flag, uint8_t *tau, const uint8_t **taued) |
| int | MMG3D_split1_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split1 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| static int | MMG3D_normalDeviation (MMG5_pMesh mesh, MMG5_int start, int8_t iface, int8_t ia, MMG5_int idx, MMG5_int ip, double n0[3]) |
| int | MMG3D_simbulgept (MMG5_pMesh mesh, MMG5_pSol met, int64_t *list, int ret, MMG5_int ip) |
| int | MMG3D_normalAdjaTri (MMG5_pMesh mesh, MMG5_int start, int8_t iface, int ia, double n[3]) |
| static int | MMG5_split1b_eltspl (MMG5_pMesh mesh, MMG5_int ip, MMG5_int k, int64_t *list, MMG5_int *newtet, uint8_t tau[4]) |
| int | MMG5_split1b (MMG5_pMesh mesh, MMG5_pSol met, int64_t *list, int ret, MMG5_int ip, int cas, int8_t metRidTyp, int8_t chkRidTet) |
| void | MMG3D_split2sf_cfg (MMG5_int flag, MMG5_int v[4], uint8_t *tau, const uint8_t **taued, uint8_t *imin) |
| int | MMG3D_split2sf_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| static int | MMG3D_crea_newTetra (MMG5_pMesh mesh, const int ne, MMG5_int *newtet, MMG5_pTetra *pt, MMG5_xTetra *xt, MMG5_pxTetra *pxt0) |
| static void | MMG3D_update_qual (MMG5_pMesh mesh, MMG5_pSol met, const int ne, MMG5_int *newtet, MMG5_pTetra *pt, int8_t metRidTyp) |
| int | MMG5_split2sf (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| int | MMG5_split2sf_globNum (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], MMG5_int vGlobNum[4], int8_t metRidTyp) |
| int | MMG3D_split2_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split2 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| int | MMG3D_split3_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split3 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| void | MMG3D_split3cone_cfg (MMG5_int flag, MMG5_int v[4], uint8_t tau[4], const uint8_t **taued, uint8_t *ia, uint8_t *ib) |
| int | MMG3D_split3cone_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split3cone (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| int | MMG5_split3cone_globNum (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], MMG5_int vGlobNum[4], int8_t metRidTyp) |
| static void | MMG3D_split3op_cfg (MMG5_pTetra pt, MMG5_int vx[6], uint8_t tau[4], const uint8_t **taued, uint8_t sym[4], uint8_t symed[6], uint8_t *ip0, uint8_t *ip1, uint8_t *ip2, uint8_t *ip3, uint8_t *ie0, uint8_t *ie1, uint8_t *ie2, uint8_t *ie3, uint8_t *ie4, uint8_t *ie5, uint8_t *imin03, uint8_t *imin12) |
| int | MMG3D_split3op_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
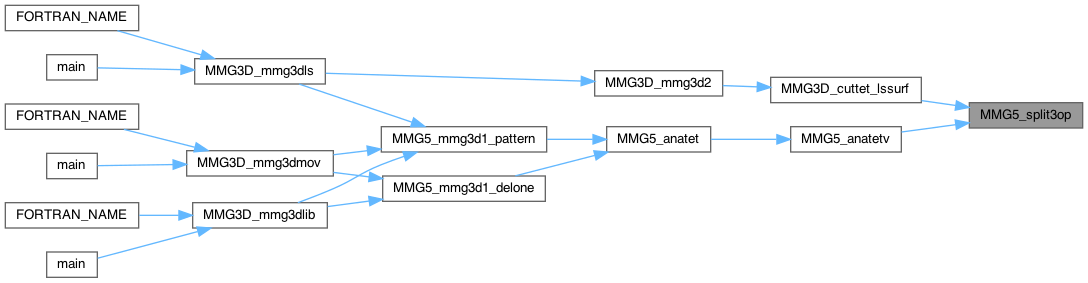
| int | MMG5_split3op (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| MMG5_int | MMG5_split4bar (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t metRidTyp) |
| static void | MMG3D_split4sf_cfg (MMG5_pTetra pt, MMG5_int vx[6], uint8_t tau[4], const uint8_t **taued, uint8_t *imin23, uint8_t *imin12) |
| int | MMG3D_split4sf_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split4sf (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| void | MMG3D_split4op_cfg (MMG5_int flag, MMG5_int v[4], uint8_t tau[4], const uint8_t **taued, uint8_t *imin01, uint8_t *imin23) |
| int | MMG3D_split4op_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split4op (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| int | MMG5_split4op_globNum (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], MMG5_int vGlobNum[4], int8_t metRidTyp) |
| static void | MMG3D_split5_cfg (MMG5_pTetra pt, MMG5_int vx[6], uint8_t tau[4], const uint8_t **taued, uint8_t *imin) |
| int | MMG3D_split5_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split5 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| int | MMG3D_split6_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6]) |
| int | MMG5_split6 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int vx[6], int8_t metRidTyp) |
| static int | MMG3D_chksplit (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int ip, int64_t *list, int ret, double crit) |
| MMG5_int | MMG5_splitedg (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int iel, int iar, double crit) |
Variables | |
| int8_t | ddb |
Functions to create new points.
Definition in file split_3d.c.
|
inlinestatic |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| ip | index of new point. |
| list | pointer to the shell of edge. |
| ret | size of the shell of edge. |
| crit | quality threshold. |
Check quality before split.
Definition at line 4862 of file split_3d.c.


|
inlinestatic |
| mesh | pointer to the mesh structure. |
| newtet | list of indices of the new tetra. |
| ne | number of tetra in the list. |
| pt | list of tetra. |
| xt | list of xtetra. |
| pxt0 | xtetra associated to the first tetra of the list |
Create a list of new tetra whose indices are passed in newtet.
Definition at line 1166 of file split_3d.c.

| int MMG3D_normalAdjaTri | ( | MMG5_pMesh | mesh, |
| MMG5_int | start, | ||
| int8_t | iface, | ||
| int | ia, | ||
| double | n[3] | ||
| ) |
| mesh | pointer to the mesh structure |
| start | index of the working tetra |
| iface | local index of the boundary face of the tetra start |
| ia | local index on face iface of the edge through which we seek the adjacent triangle of the triangle iface of start. |
| n | normal of the new boundary face in the tetra idx. |
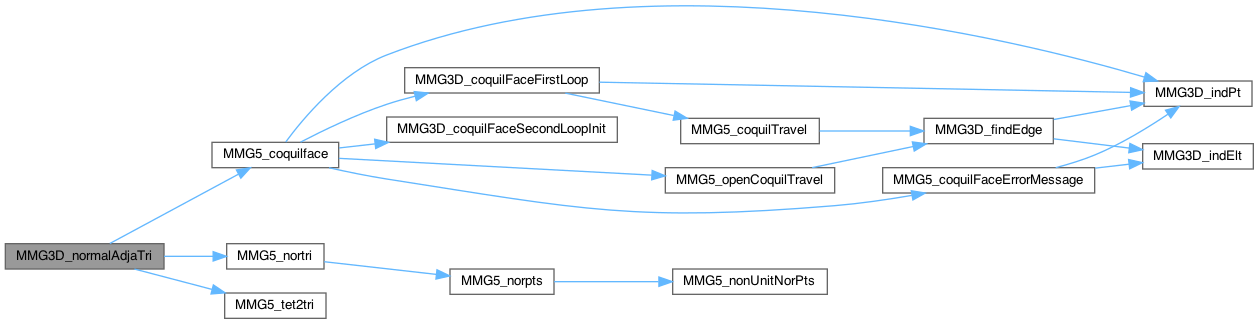
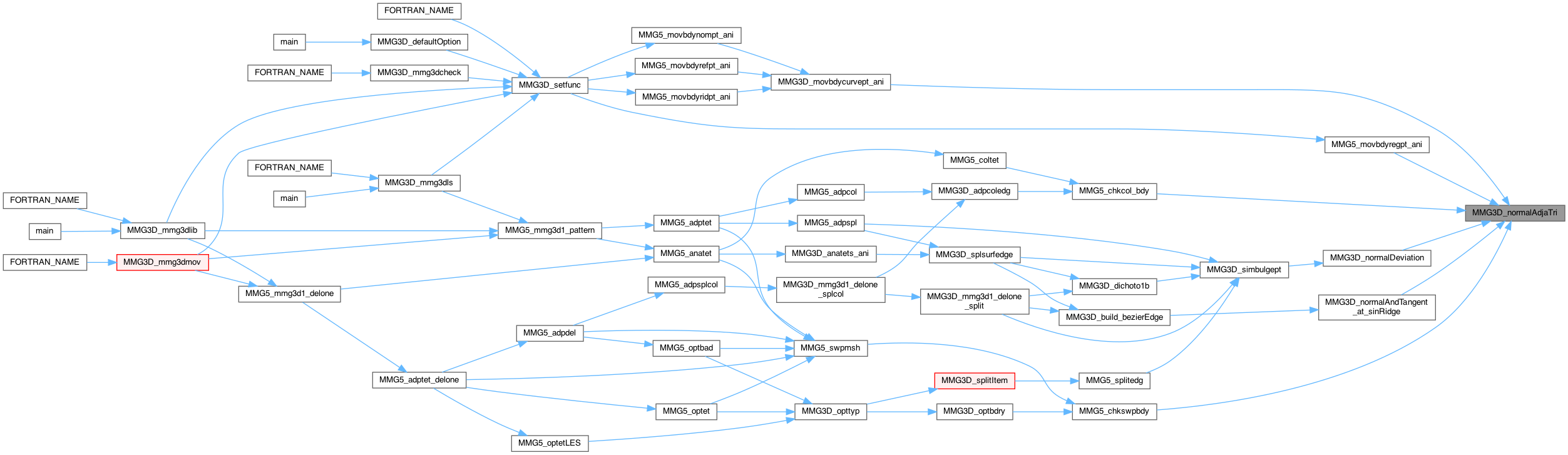
Compute the normal of the adjacent triangle of the triangle iface of the tetra start through the edge ia (in local numbering of the face).
Store the adjacent boundary triangle (triangle adjacent to iface through the edge ia
Compute the normal of the second triangle
Definition at line 472 of file split_3d.c.
|
inlinestatic |
| mesh | pointer to the mesh structure |
| start | index of the tetra that we want to split |
| iface | local index of the boundary face that we want to split |
| ia | local index of the boundary edge that we want to split |
| idx | local index of the new tetra that we want to study after the splitting of the tetra start (idx=0 or 1) |
| ip | new point index |
| n0 | normal of the new boundary face in the tetra idx. |
Check that the split of the edge ia of the tetra start does not create a ridge along the \( idx^{th} \) edge opposite to ip in the boundary triangle iface. Store the normal of the \( idx^{th} \) boundary triangle in n0.
Store the first boundary triangle (the one that is created in the boundary face that we split)
Compute the normal of the first triangle
Compute the normal of the second triangle (triangle adjacent to the first through the edge iploc)
Definition at line 272 of file split_3d.c.


| int MMG3D_simbulgept | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| int64_t * | list, | ||
| int | ret, | ||
| MMG5_int | ip | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric. |
| list | pointer to the edge shell. |
| ret | size of the edge shell. |
| ip | new point index. |
Simulate at the same time creation and bulging of one point, with new position o and tag tag, to be inserted at an edge, whose shell is passed.
Check the deviation for new triangles
Definition at line 330 of file split_3d.c.


|
inline |
| flag | flag to detect the splitting configuration |
| tau | vertices permutation |
| taued | edges permutation |
Compute vertices and edges permutation for the split of 1 edge depending of the edge that is splitted (i^th bit of flag is 1 if the i^th edge is splitted).
Definition at line 53 of file split_3d.c.
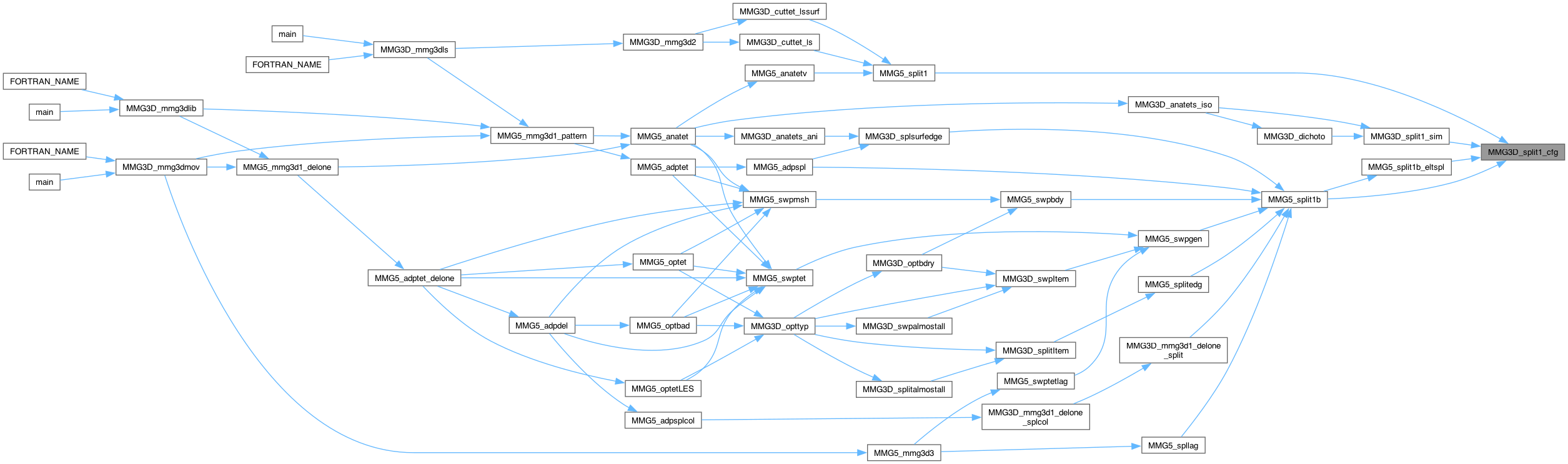
| int MMG3D_split1_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate the splitting of 1 edge of element
Definition at line 94 of file split_3d.c.

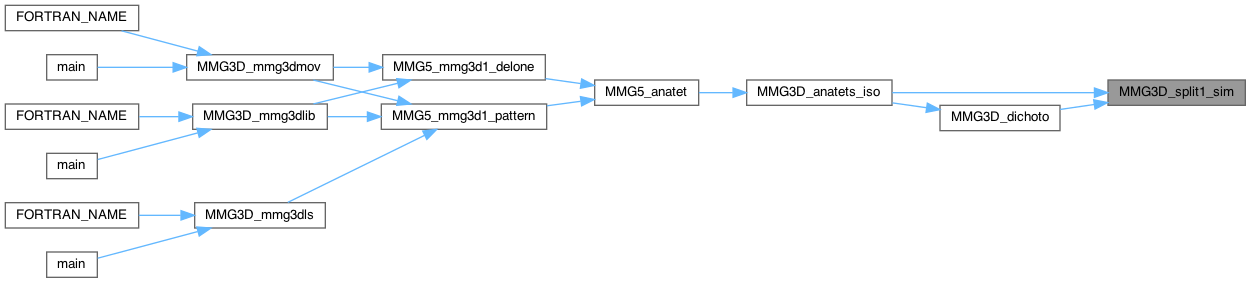
| int MMG3D_split2_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate split of two opposite edges.
Definition at line 1427 of file split_3d.c.

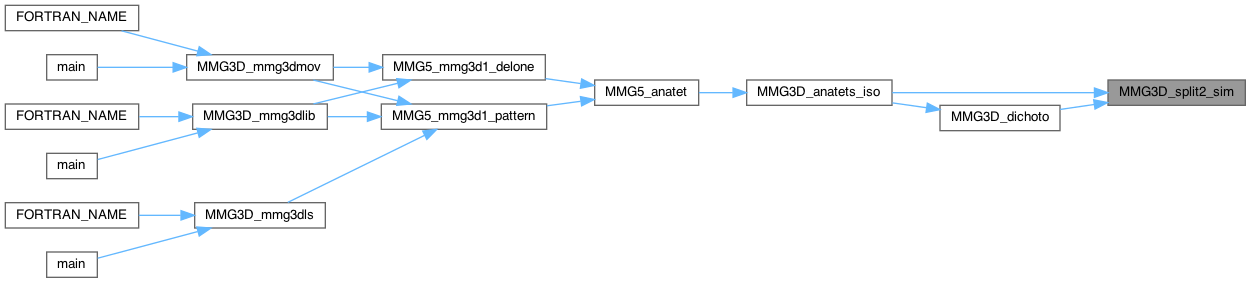
|
inline |
| flag | flag to detect the splitting configuration |
| v | indices of the tetra nodes (global node indices if called from ParMmg in ls mode) |
| tau | vertices permutation |
| taued | edges permutation |
Compute vertices and edges permutation for the split of 2 edge along the same face. The configuration flag is computed such as the i^th bit of flag is 1 if the i^th edge is splitted).
Definition at line 1037 of file split_3d.c.

| int MMG3D_split2sf_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate split of two edges that belong to a common face
Definition at line 1103 of file split_3d.c.

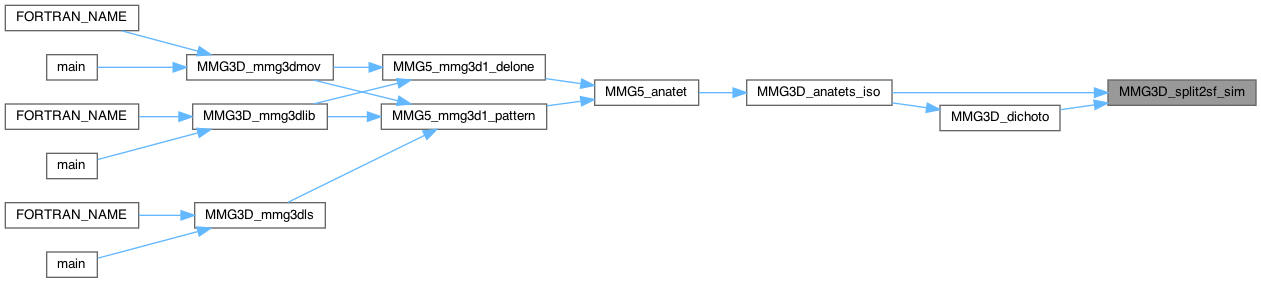
| int MMG3D_split3_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
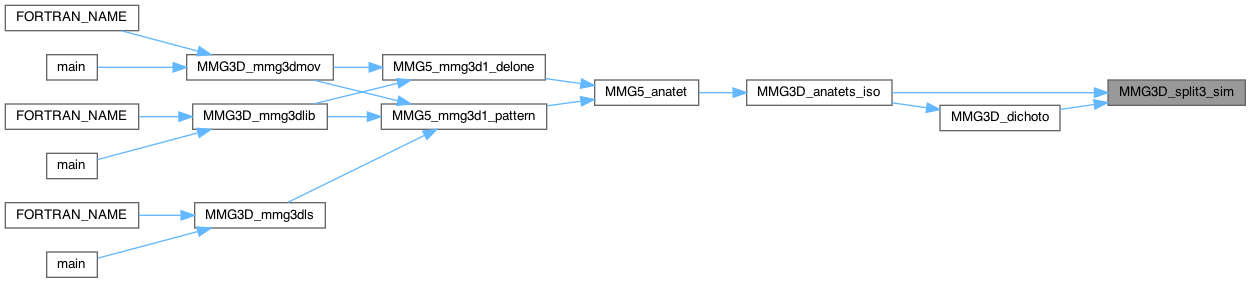
Simulate split of 1 face (3 edges)
Definition at line 1636 of file split_3d.c.

|
inline |
| flag | initial tetra |
| v | indices of the tetra nodes (global node indices if called from ParMmg in ls mode) |
| tau | vertices permutation |
| taued | edges permutation |
| ia | first condition to choose the split |
| ib | second condition to choose the split |
Set permutation of vertices for the split of 3 edges in cone configuration. Reference configuration 7.
Definition at line 1863 of file split_3d.c.

| int MMG3D_split3cone_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
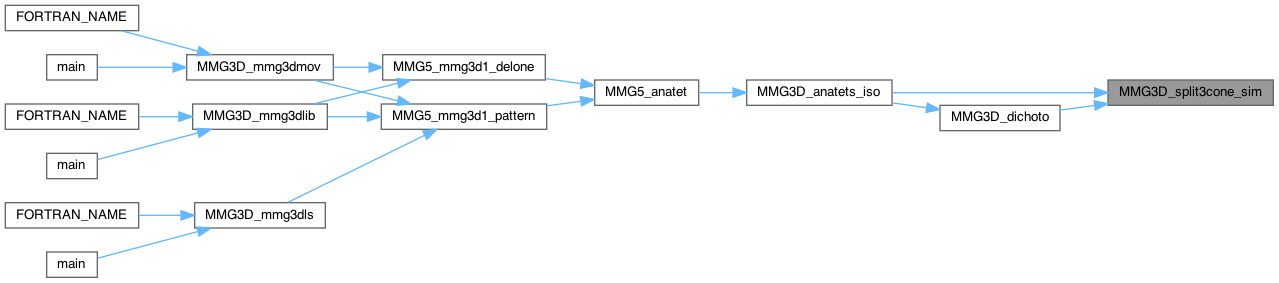
Simulate split of 3 edges in cone configuration.
Definition at line 1921 of file split_3d.c.

|
inlinestatic |
| pt | initial tetra |
| vx | index of points to insert along edges |
| tau | vertices permutation |
| taued | edges permutation |
| sym | vertices symmetry |
| symed | edges symmetry |
| ip0 | vertex 0 for reference config |
| ip1 | vertex 1 for reference config |
| ip2 | vertex 2 for reference config |
| ip3 | vertex 3 for reference config |
| ie0 | edge 0 for reference config |
| ie1 | edge 1 for reference config |
| ie2 | edge 2 for reference config |
| ie3 | edge 3 for reference config |
| ie4 | edge 4 for reference config |
| ie5 | edge 5 for reference config |
| imin03 | minimal index of vertices ip0 and ip3 |
| imin12 | minimal index of vertices ip1 and ip2 |
Set permutation /symmetry of vertices for 3 opposite edges config: generic case : 35
Definition at line 2365 of file split_3d.c.

| int MMG3D_split3op_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
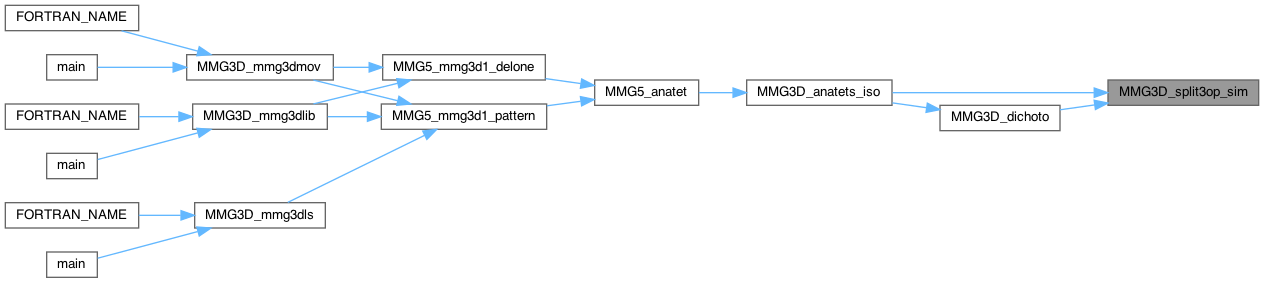
Simulate split of 3 edges in opposite configuration.
Definition at line 2522 of file split_3d.c.

|
inline |
| flag | initial tetra |
| v | indices of tetra nodes (global node indices if called from ParMmg in ls mode) |
| tau | vertices permutation |
| taued | edges permutation |
| imin01 | minimal index of vertices ip0 and ip1 |
| imin23 | minimal index of vertices ip2 and ip3 |
Set permutation of vertices for the split of 4 edges when on opposite edges. Reference configuration 30.
Definition at line 3649 of file split_3d.c.

| int MMG3D_split4op_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
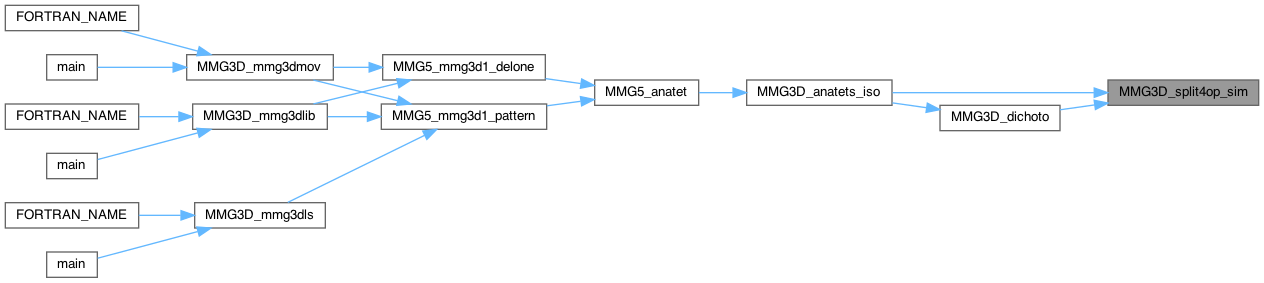
Simulate split of 4 edges in opposite configuration.
Definition at line 3685 of file split_3d.c.

|
inlinestatic |
| pt | initial tetra |
| vx | index of points to insert along edges |
| tau | vertices permutation |
| taued | edges permutation |
| imin23 | minimal index of vertices ip0 and ip3 |
| imin12 | minimal index of vertices ip1 and ip2 |
Set permutation of vertices for the split of 4 edges when 3 lie on the same face. Reference configuration 23
Definition at line 3260 of file split_3d.c.

| int MMG3D_split4sf_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate split of 4 edges in a configuration when 3 lie on the same face.
Definition at line 3337 of file split_3d.c.

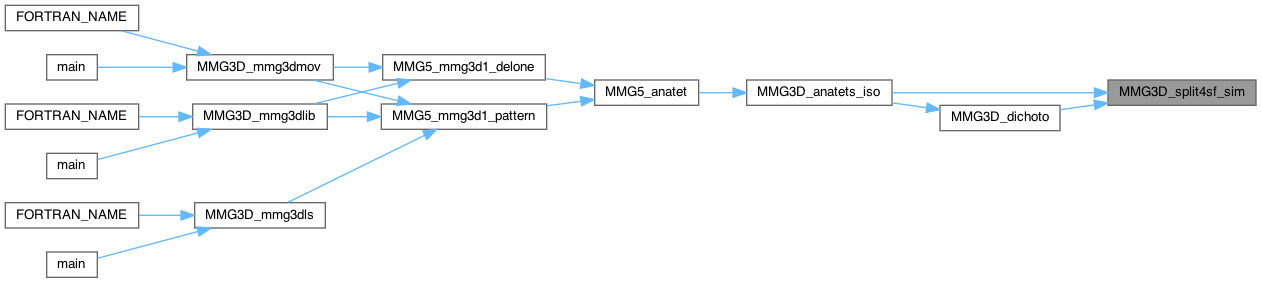
|
inlinestatic |
| pt | initial tetra |
| vx | index of points to insert along edges |
| tau | vertices permutation |
| taued | edges permutation |
| imin | minimal index of vertices tau[0] and tau[1] |
Set permutation of vertices for the split of 5 edges. Reference configuration is 62.
Definition at line 4062 of file split_3d.c.

| int MMG3D_split5_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate split of 5 edges.
Definition at line 4111 of file split_3d.c.

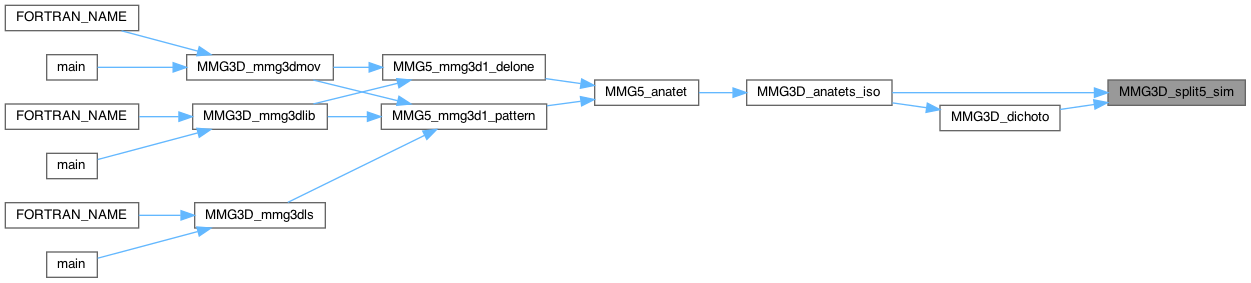
| int MMG3D_split6_sim | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6] | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
Simulate split of 6 edges.
Definition at line 4414 of file split_3d.c.

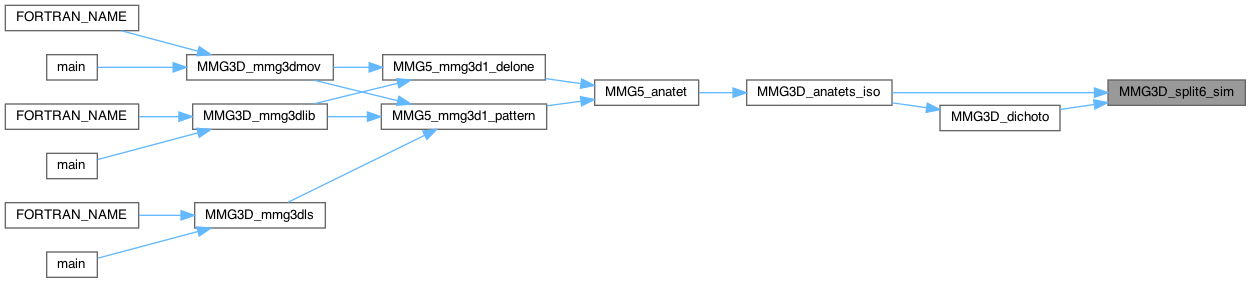
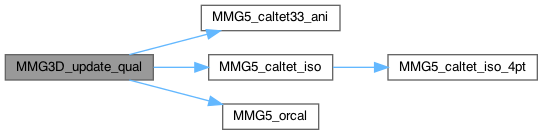
|
inlinestatic |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| ne | number of tetra in the list |
| newtet | list of tetra indices |
| pt | list of tetra |
| metRidTyp | metric storage (classic or special) |
Compute the quality of the nnew tetra of the list pt.
Definition at line 1219 of file split_3d.c.
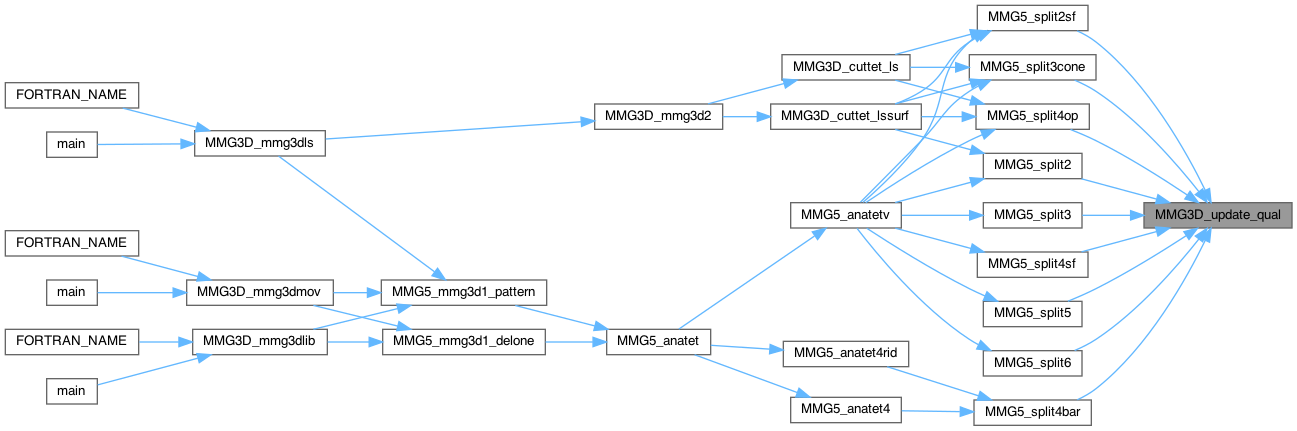
| int MMG5_split1 | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
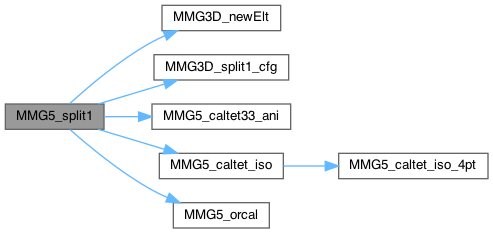
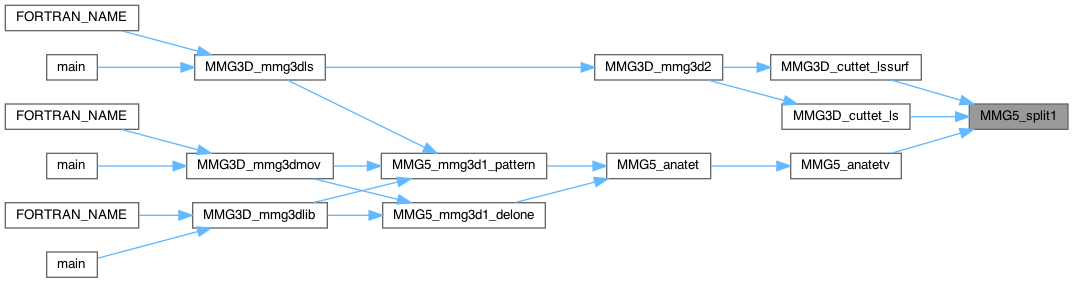
Split 1 edge of tetra k.
Definition at line 134 of file split_3d.c.
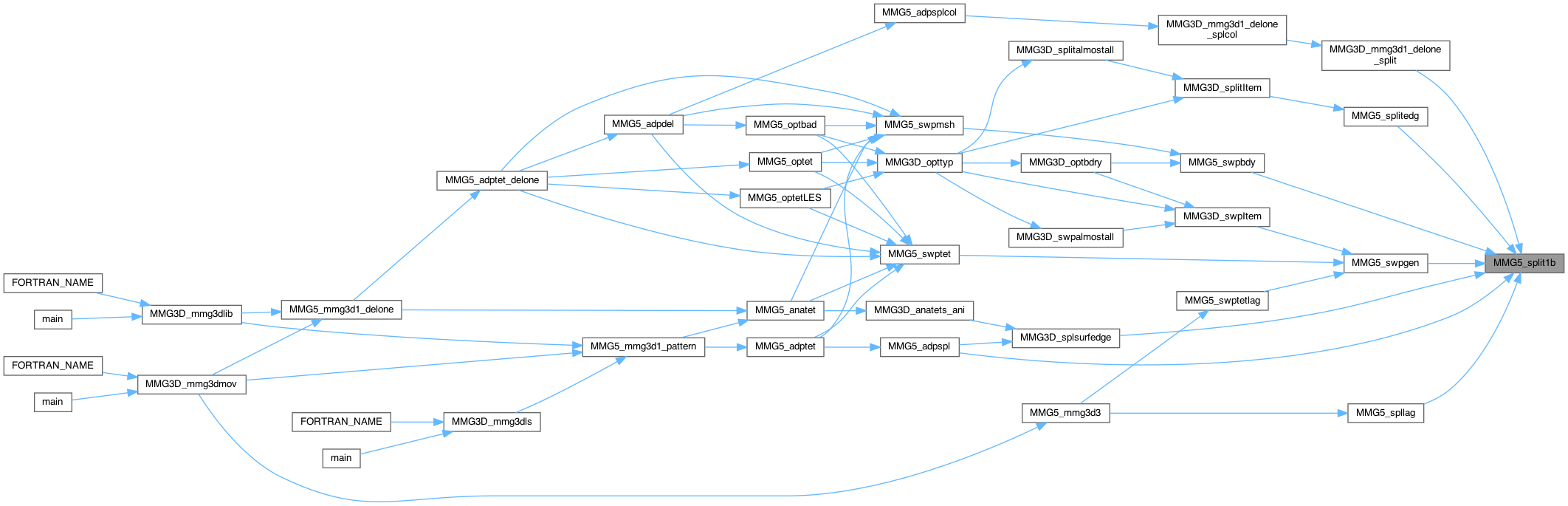
| int MMG5_split1b | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| int64_t * | list, | ||
| int | ret, | ||
| MMG5_int | ip, | ||
| int | cas, | ||
| int8_t | metRidTyp, | ||
| int8_t | chkRidTet | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| list | pointer to the shell of edge. |
| ret | size of the shell of edge. |
| ip | idex of new point. |
| cas | flag to watch the length of the new edges. |
| metRidTyp | Type of storage of ridges metrics: 0 for classic storage, 1 for special storage. |
| chkRidTet | if 1, avoid the creation of a tet with 4 ridge vertices |
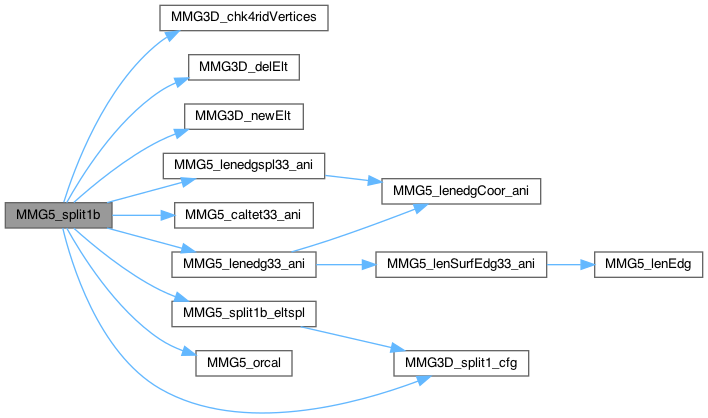
Split edge \(list[0]\%6\), whose shell list is passed, introducing point ip Beware : shell has to be enumerated in ONLY ONE TRAVEL (always same sense).
2 different checks : 1) are we creating a too small edge (BUG_Split1b_SpereIso_0.125h_met) 2) in aniso and from the last wave of anatet(typchk=1): avoid the creation of a tetra with 4 ridge vertices.
Definition at line 629 of file split_3d.c.
|
inlinestatic |
| mesh | pointer to the mesh structure. |
| ip | index of new point. |
| k | position of the tetra to split in the shell of edge. |
| list | pointer to the shell of edge. |
| newtet | list of indices of created tetra |
| tau | vertices permutation |
Update and fill the tetra and xtetra data when splitting one edge of a tetra.
Definition at line 519 of file split_3d.c.

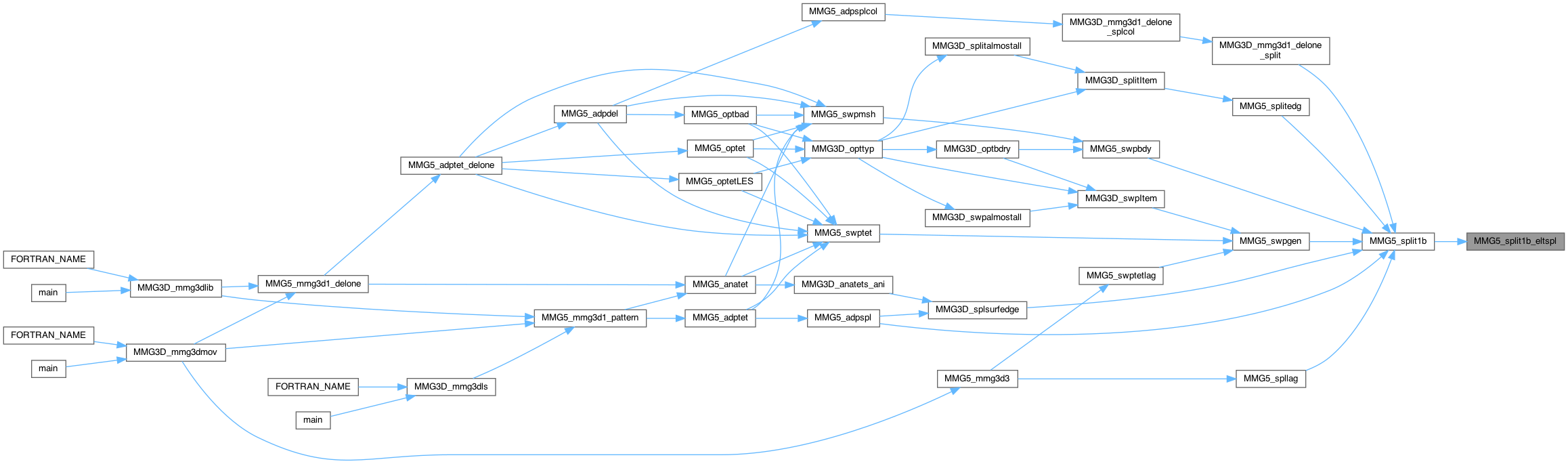
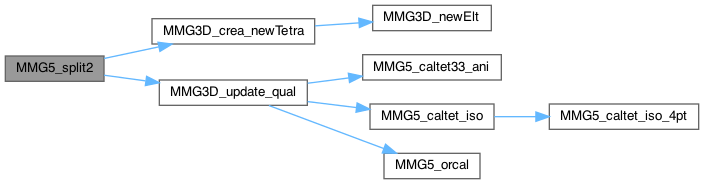
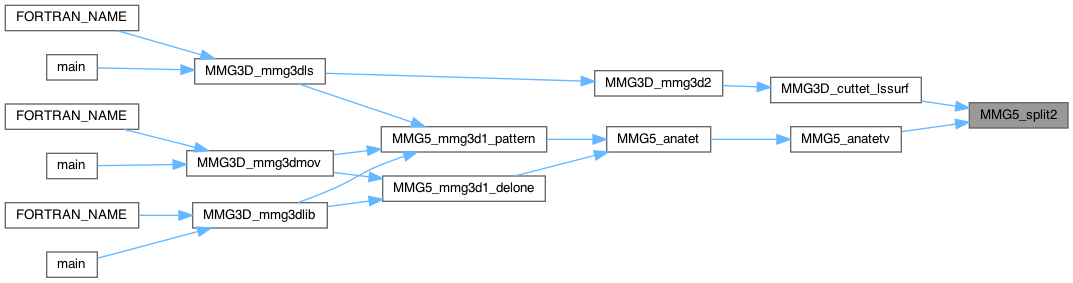
| int MMG5_split2 | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split of two OPPOSITE edges
Definition at line 1489 of file split_3d.c.
| int MMG5_split2sf | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split of two edges that belong to a common face : 1 tetra becomes 3
Definition at line 1254 of file split_3d.c.
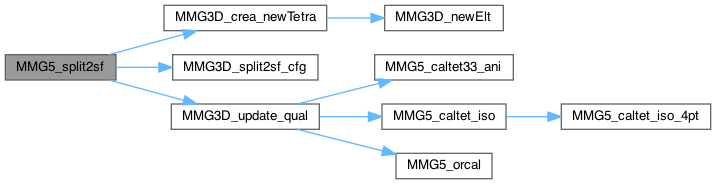
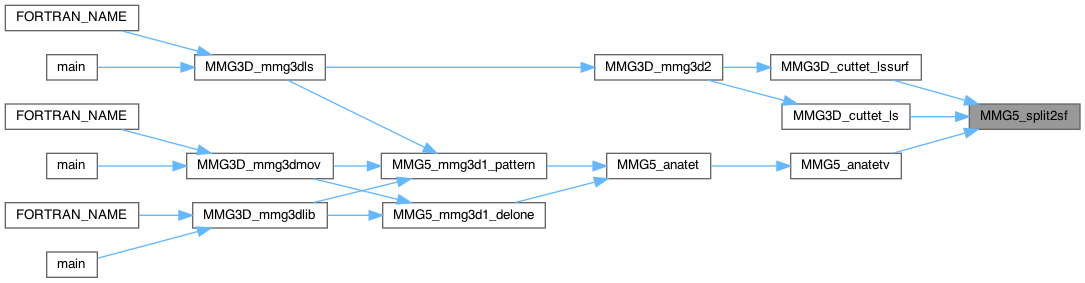
| int MMG5_split2sf_globNum | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| MMG5_int | vGlobNum[4], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| vGlobNum | vertices indices of the tetra k (global node indices if called from ParMmg in ls mode). |
| metRidTyp | metric storage (classic or special) |
Split of two edges that belong to a common face : 1 tetra becomes 3
Definition at line 1276 of file split_3d.c.

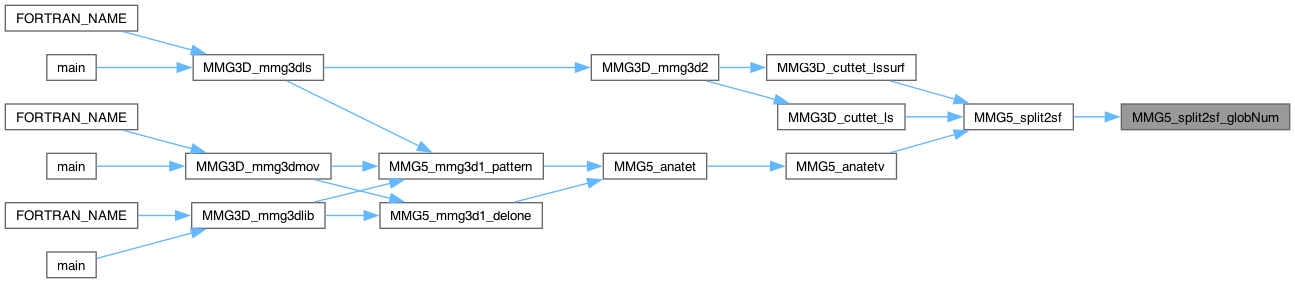
| int MMG5_split3 | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
1 face (3 edges) subdivided
Definition at line 1707 of file split_3d.c.
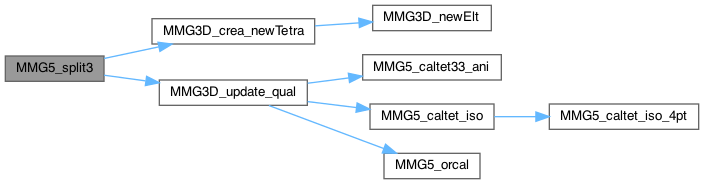
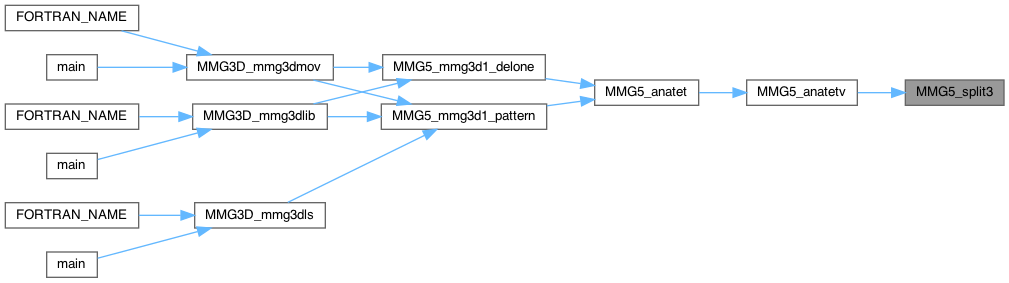
| int MMG5_split3cone | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split 3 edge in cone configuration
Definition at line 2059 of file split_3d.c.
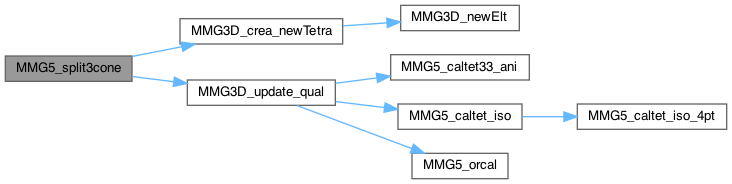
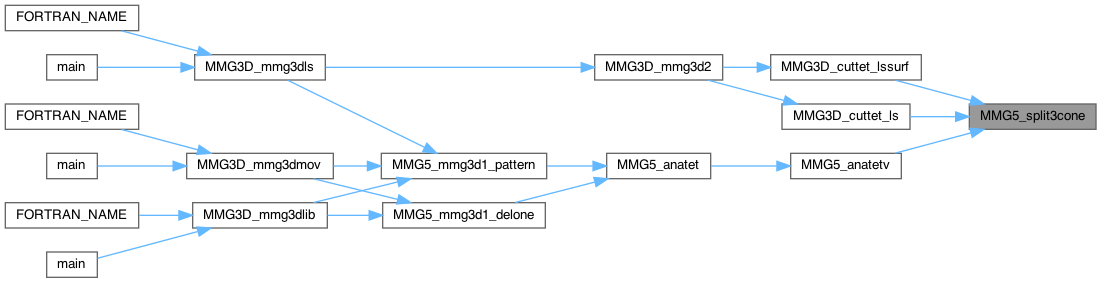
| int MMG5_split3cone_globNum | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| MMG5_int | vGlobNum[4], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| vGlobNum | vertices indices of the tetra k (global node indices if called from ParMmg in ls mode). |
| metRidTyp | metric storage (classic or special) |
Split 3 opposite edges in a tetra
Definition at line 2081 of file split_3d.c.
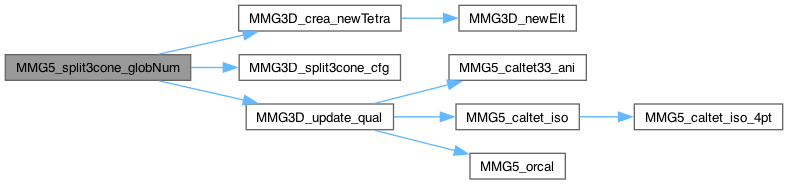
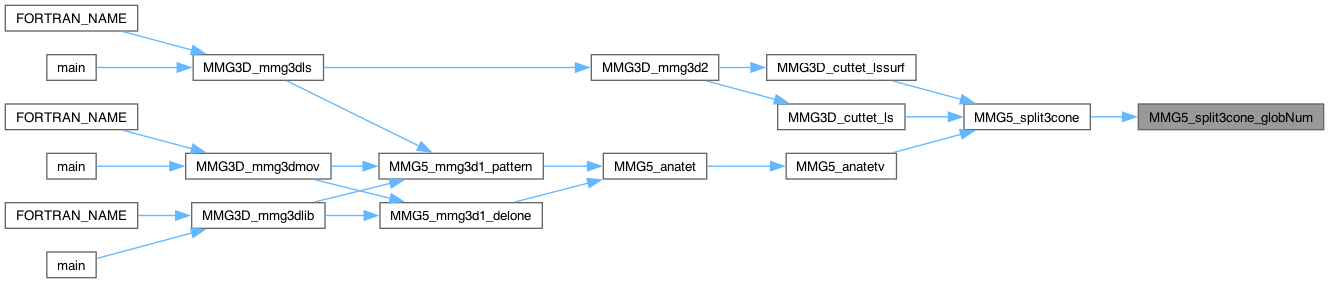
| int MMG5_split3op | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split 3 opposite edges in a tetra
Definition at line 2654 of file split_3d.c.
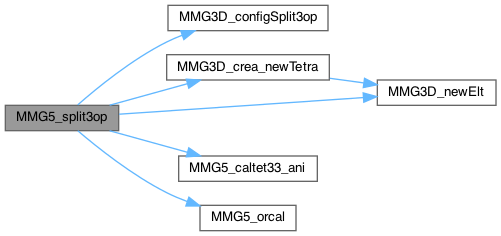
| MMG5_int MMG5_split4bar | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | tetra index. |
| metRidTyp | metric storage (classic or special) |
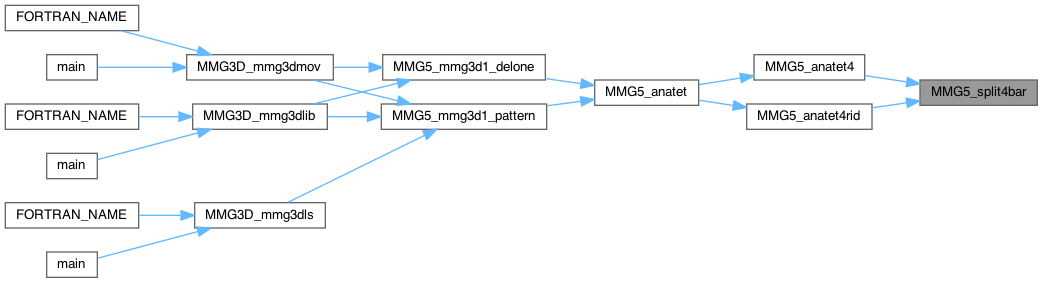
Split a tetra in 4 tetras by introducing its barycenter. FOR NOW : flags, that tell which edge should be split, are not updated (erased) : UPDATE NEEDED ?
Definition at line 3050 of file split_3d.c.
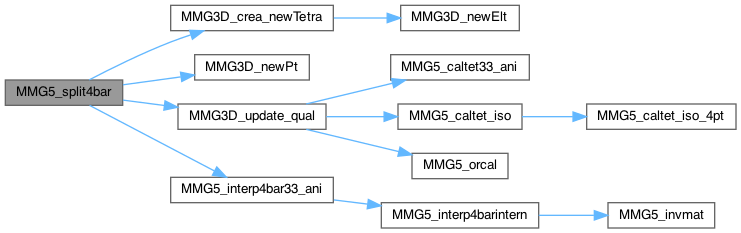
| int MMG5_split4op | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
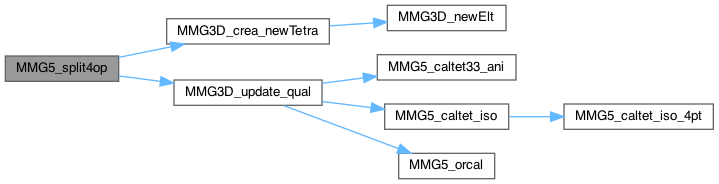
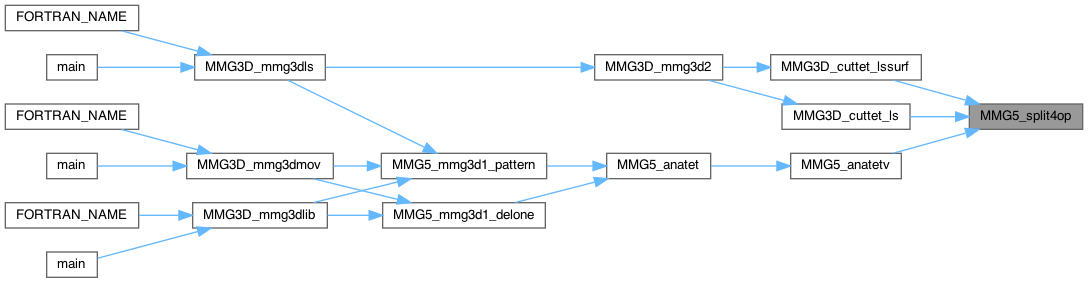
Split 4 edges in a configuration when no 3 edges lie on the same face
Definition at line 3804 of file split_3d.c.
| int MMG5_split4op_globNum | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| MMG5_int | vGlobNum[4], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| vGlobNum | vertices indices of the tetra k (global node indices if called from ParMmg in ls mode). |
| metRidTyp | metric storage (classic or special) |
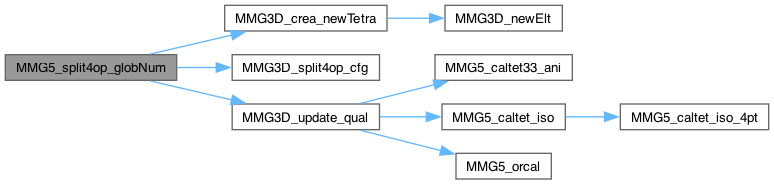
Split 4 edges in a configuration when no 3 edges lie on the same face
Definition at line 3826 of file split_3d.c.
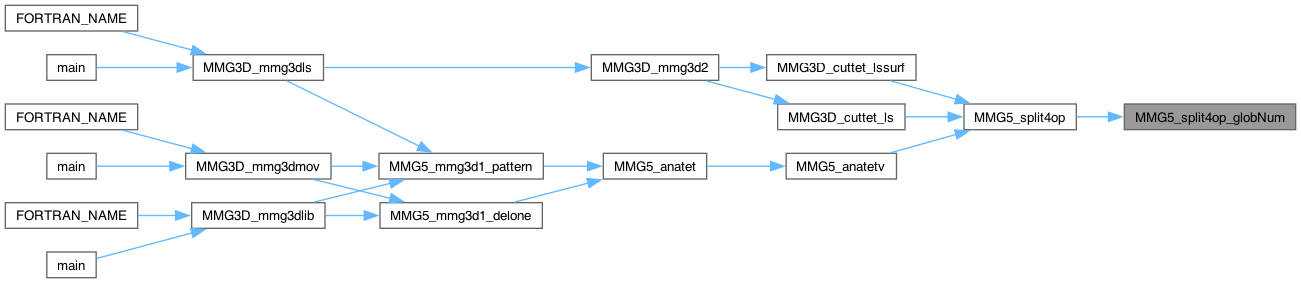
| int MMG5_split4sf | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split 4 edges in a configuration when 3 lie on the same face
Definition at line 3440 of file split_3d.c.
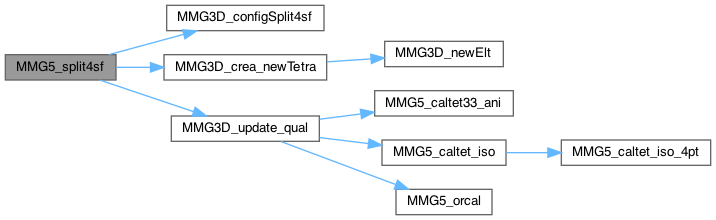
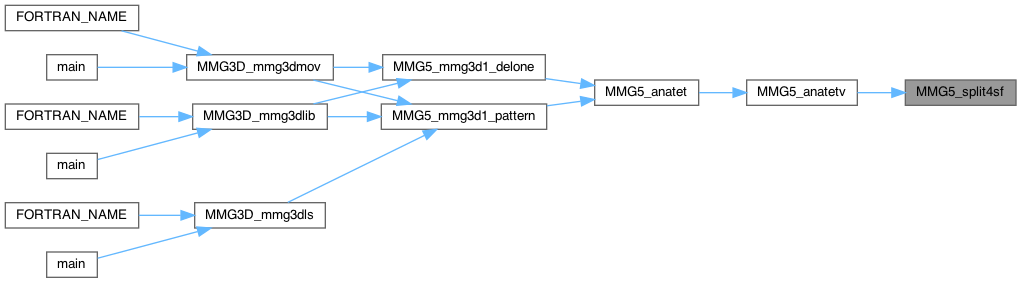
| int MMG5_split5 | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
Split 5 edges
Definition at line 4203 of file split_3d.c.
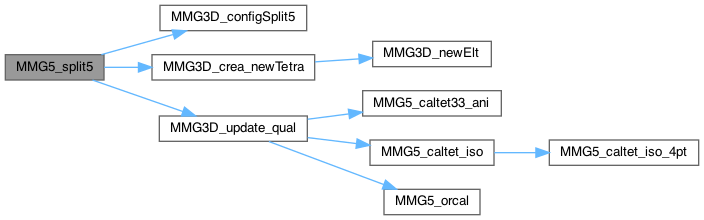
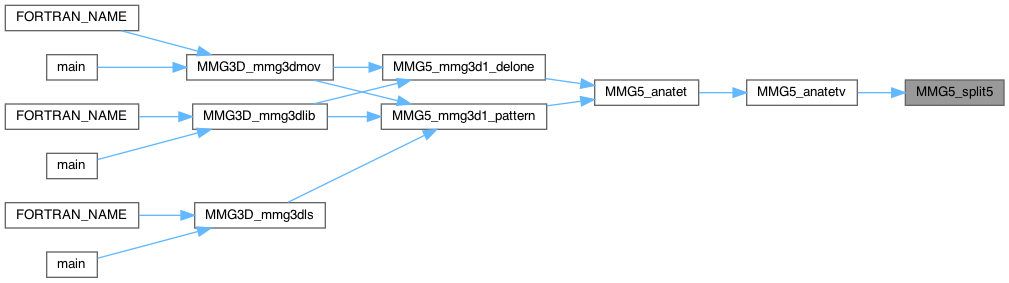
| int MMG5_split6 | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | k, | ||
| MMG5_int | vx[6], | ||
| int8_t | metRidTyp | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| k | index of element to split. |
| vx | \(vx[i]\) is the index of the point to add on the edge i. |
| metRidTyp | metric storage (classic or special) |
split all faces (6 edges)
Definition at line 4483 of file split_3d.c.

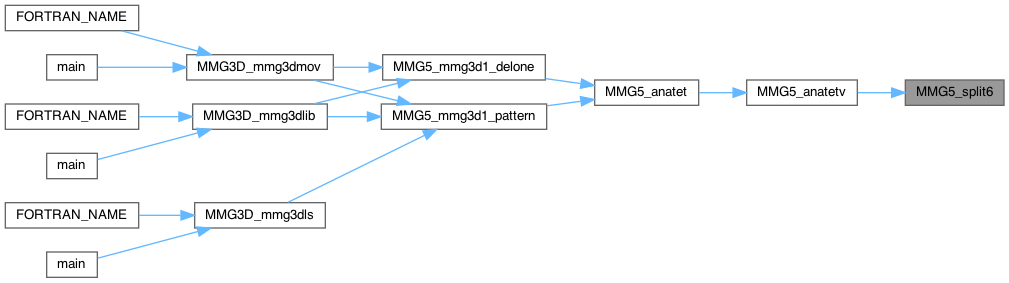
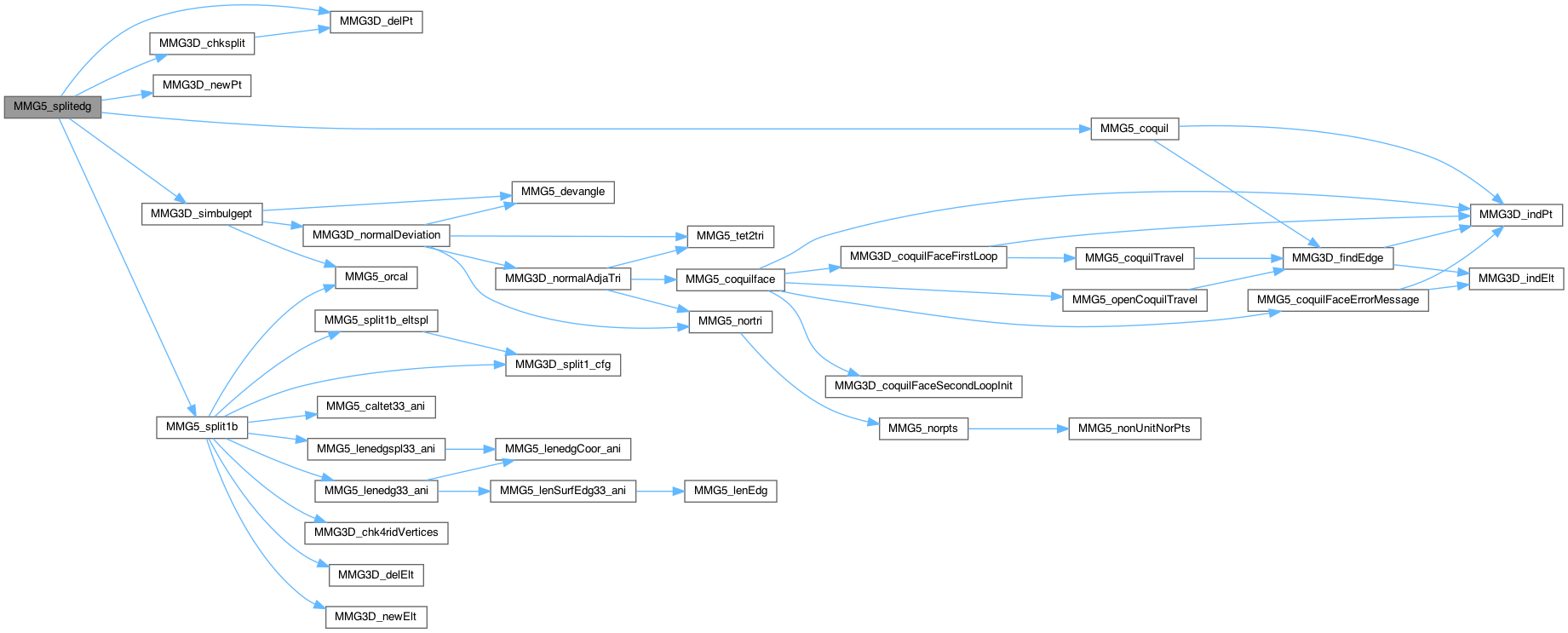
| MMG5_int MMG5_splitedg | ( | MMG5_pMesh | mesh, |
| MMG5_pSol | met, | ||
| MMG5_int | iel, | ||
| int | iar, | ||
| double | crit | ||
| ) |
| mesh | pointer to the mesh structure. |
| met | pointer to the metric structure. |
| iel | tetra index |
| iar | edge index of iel |
| crit | quality threshold. |
Split edge iar of iel and verify that every new tet have a better quality than crit
Definition at line 4916 of file split_3d.c.

|
extern |
Definition at line 42 of file mmg3d1_delone.c.