Tools functions for the mmgs library. More...

#include "libmmgs.h"
#include "libmmgs_private.h"
#include "inlined_functions_private.h"
#include "mmgsexterns_private.h"
#include "mmgexterns_private.h"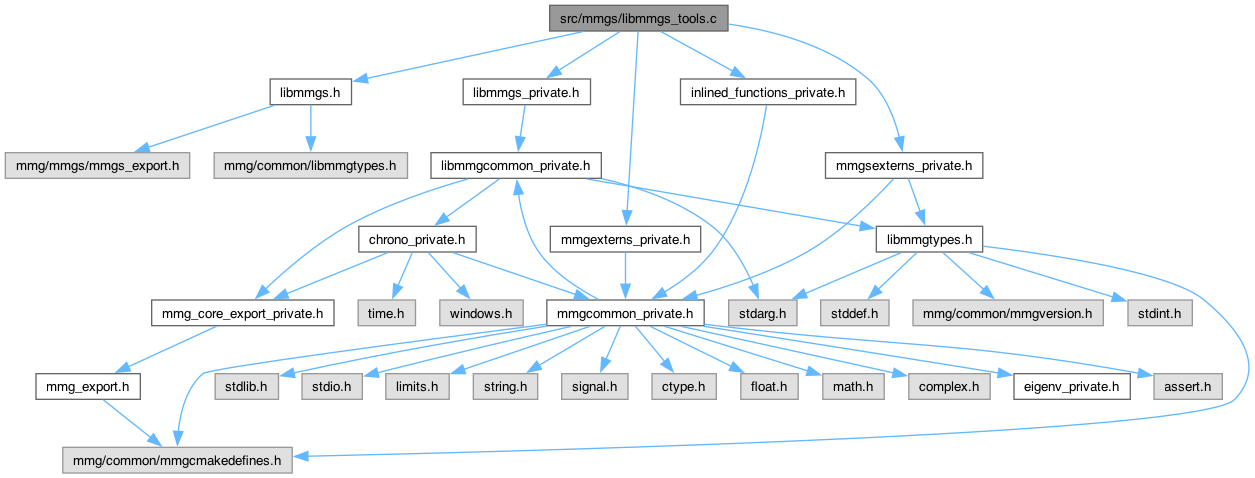

Include dependency graph for libmmgs_tools.c:

Go to the source code of this file.

Functions
void	MMGS_setfunc (MMG5_pMesh mesh, MMG5_pSol met)
	Set function pointers for caltet, lenedg, defsiz and gradsiz.

int	MMGS_usage (char *prog)
	Print help for mmgs options.

int	MMGS_defaultValues (MMG5_pMesh mesh)
	Print the default parameter values.

int	MMGS_parsar (int argc, char *argv[], MMG5_pMesh mesh, MMG5_pSol met, MMG5_pSol sol)
	Store command line arguments.

int	MMGS_freeLocalPar (MMG5_pMesh mesh)

int	MMGS_stockOptions (MMG5_pMesh mesh, MMG5_Info *info)
	Store the info structure in the mesh structure.

void	MMGS_destockOptions (MMG5_pMesh mesh, MMG5_Info *info)
	Recover the info structure stored in the mesh structure.

int	MMGS_Get_numberOfNonBdyEdges (MMG5_pMesh mesh, MMG5_int *nb_edges)
	Get the number of non-boundary edges.

int	MMGS_Get_nonBdyEdge (MMG5_pMesh mesh, MMG5_int e0, MMG5_int e1, MMG5_int *ref, MMG5_int idx)
	Get vertices and reference of a non-boundary edge.

int	MMGS_Get_adjaTri (MMG5_pMesh mesh, MMG5_int kel, MMG5_int listri[3])
	Return adjacent triangles of a triangle.

int	MMGS_Get_adjaVerticesFast (MMG5_pMesh mesh, MMG5_int ip, MMG5_int start, MMG5_int lispoi[MMGS_LMAX])
	Find adjacent vertices of a triangle.

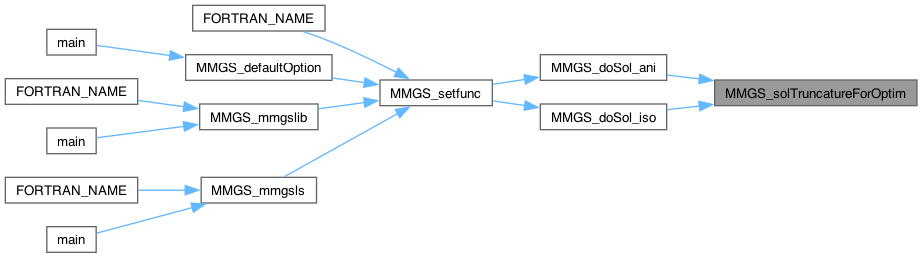
static int	MMGS_solTruncatureForOptim (MMG5_pMesh mesh, MMG5_pSol met, int ani)

int	MMGS_doSol_iso (MMG5_pMesh mesh, MMG5_pSol met)

static int	MMGS_unitTensor_3D (MMG5_pMesh mesh, MMG5_int k, int i, MMG5_pPoint p1, double *m)

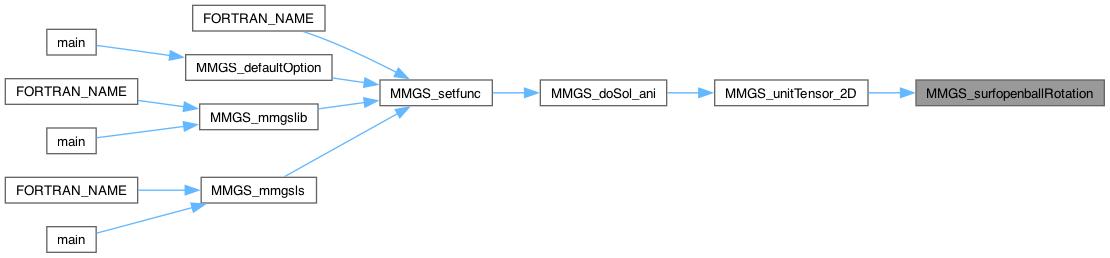
static int	MMGS_surfopenballRotation (MMG5_pMesh mesh, MMG5_pPoint p0, MMG5_int k, int i, int ilist, double r[3][3], double *lispoi, double n[3])

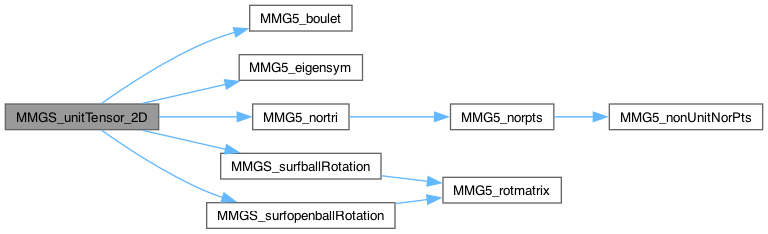
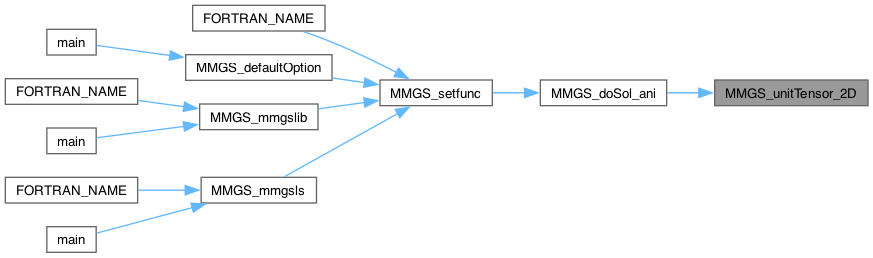
static int	MMGS_unitTensor_2D (MMG5_pMesh mesh, MMG5_int k, int i, MMG5_pPoint p1, double *m, double isqhmax)

int	MMGS_doSol_ani (MMG5_pMesh mesh, MMG5_pSol met)

int	MMGS_Set_constantSize (MMG5_pMesh mesh, MMG5_pSol met)
	Compute a constant size map.

int	MMGS_Compute_eigenv (double m[6], double lambda[3], double vp[3][3])
	Compute the real eigenvalues and eigenvectors of a symmetric matrix.

void	MMGS_Free_solutions (MMG5_pMesh mesh, MMG5_pSol sol)
	Free a solution.

int	MMGS_Clean_isoSurf (MMG5_pMesh mesh)
	Clean data (triangles and edges) linked to isosurface.

Detailed Description

Tools functions for the mmgs library.

Author: Charles Dapogny (UPMC); Cécile Dobrzynski (Bx INP/Inria/UBordeaux); Pascal Frey (UPMC); Algiane Froehly (Inria/UBordeaux)

Version: 5

Copyright: GNU Lesser General Public License.

Todo:: Doxygen documentation

Definition in file libmmgs_tools.c.

Function Documentation

◆ MMGS_Clean_isoSurf()

int MMGS_Clean_isoSurf ( MMG5_pMesh mesh )

Clean data (triangles and edges) linked to isosurface.

Parameters

mesh	pointer to mesh structure

Returns: 1 if successful, 0 otherwise.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_CLEAN_ISOSURF(mesh,retval)
MMG5_DATA_PTR_T, INTENT(IN) :: mesh
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 1640 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Compute_eigenv()

int MMGS_Compute_eigenv	(	double	m[6],
		double	lambda[3],
		double	vp[3][3]
	)

Compute the real eigenvalues and eigenvectors of a symmetric matrix.

Parameters

m	upper part of a symmetric matrix diagonalizable in \|R
lambda	array of eigenvalues
vp	array of eigenvectors

Returns: the order of the eigenvalues

Compute the real eigenvalues and eigenvectors of a symmetric matrix m whose upper part is provided (m11, m12, m13, m22, m23, m33 in this order).

lambda[0] is the eigenvalue associated to the eigenvector ( v[0][0], v[0,1], v[0,2] ) in C and to the eigenvector v(1,:) in fortran

lambda[1] is the eigenvalue associated to the eigenvector ( v[1][0], v[1,1], v[1,2] ) in C and to the eigenvector v(2,:) in fortran

lambda[2] is the eigenvalue associated to the eigenvector ( v[2][0], v[2,1], v[2,2] ) in C and to the eigenvector v(3,:) in fortran

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_COMPUTE_EIGENV(m,lambda,vp,retval)
REAL(KIND=8), INTENT(IN) :: m(*)
REAL(KIND=8), INTENT(OUT) :: lambda(*),vp(*)
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 1607 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_defaultValues()

int MMGS_defaultValues ( MMG5_pMesh mesh )

Print the default parameter values.

Parameters

mesh	pointer to the mesh structure.

Returns: 0 on failure, 1 on success.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_DEFAULTVALUES(mesh,retval)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 111 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_destockOptions()

void MMGS_destockOptions	(	MMG5_pMesh	mesh,
		MMG5_Info *	info
	)

Recover the info structure stored in the mesh structure.

Parameters

mesh	pointer to the mesh structure.
info	pointer to the info structure.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_DESTOCKOPTIONS(mesh,info)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh,info
END SUBROUTINE

Definition at line 565 of file libmmgs_tools.c.

Here is the caller graph for this function:

◆ MMGS_doSol_ani()

int MMGS_doSol_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns: 1 if succeed, 0 if fail

Remarks: need the normal at vertices.; hmax/hmin may be not setted here so we can't use it.

Compute the unit metric tensor at mesh vertices (from edges passing through the vertices).

Increment base marker to detect points already processed

Step 1: treat non-manifold points: travel triangle edges and add edge contribution to extremities (we have to do that because ball of non-manifold points can't be computed)

Corner point (no normal at vertex): if the corner defines an angle we can compute the 3D unit tensor (non singular), in the other cases (corner along a flat surface, for example because it is at the intersection of 3 specific edges or because it is provided by the user) we will project the edges onto the tangent plane and compute the 2D unit tensor (as for required and regular points)

Required point (no normal at vertex): projection of edges onto the tangent plane and computation of the 2D unit tensor

Ridge point (2 normals): normally we can compute the 3D unit tensor. If the angle is too flat, the computation fails and we try to compute the 2D unit tensor on the tangent plane of the point.

Regular or reference point: projection of edges onto the tangent plane and computation of the 2D unit metric tensor

Step 3: check computed metric

Step 4: computation of hmin/hmax (if needed) and metric truncature

Definition at line 1334 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_doSol_iso()

int MMGS_doSol_iso	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns: 1 if succeed, 0 if fail

Remarks: need the normal at vertices.

Compute isotropic size map according to the mean of the length of the edges passing through a point.

Definition at line 859 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Free_solutions()

void MMGS_Free_solutions	(	MMG5_pMesh	mesh,
		MMG5_pSol	sol
	)

Free a solution.

Parameters

mesh	pointer to the mesh structure
sol	pointer to the solution structure

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_FREE_SOLUTIONS(mesh,sol)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh,sol
END SUBROUTINE

Definition at line 1613 of file libmmgs_tools.c.

Here is the caller graph for this function:

◆ MMGS_freeLocalPar()

int MMGS_freeLocalPar ( MMG5_pMesh mesh )

Definition at line 544 of file libmmgs_tools.c.

◆ MMGS_Get_adjaTri()

int MMGS_Get_adjaTri	(	MMG5_pMesh	mesh,
		MMG5_int	kel,
		MMG5_int	listri[3]
	)

Return adjacent triangles of a triangle.

Parameters

mesh	pointer to the mesh structure.
kel	triangle index.
listri	pointer to the array of indices of the three adjacent triangles of triangle kel (the index is 0 if there is no adjacent triangle).

Returns: 1.

Find the indices of the 3 adjacent elements of triangle kel. \(v_i = 0\) if the \(i^{th}\) face has no adjacent element (so we are on a boundary face).

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_GET_ADJATRI(mesh,kel,listri,retval)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh
INTEGER(MMG5F_INT), INTENT(IN) :: kel
INTEGER(MMG5F_INT), DIMENSION(3), INTENT(OUT) :: listri
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 709 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Get_adjaVerticesFast()

int MMGS_Get_adjaVerticesFast	(	MMG5_pMesh	mesh,
		MMG5_int	ip,
		MMG5_int	start,
		MMG5_int	lispoi[MMGS_LMAX]
	)

Find adjacent vertices of a triangle.

Parameters

mesh	pointer to the mesh structure.
ip	vertex index.
start	index of a triangle holding ip.
lispoi	pointer to an array of size MMGS_LMAX that will contain the indices of adjacent vertices to the vertex ip.

Returns: nbpoi the number of adjacent vertices on success, 0 on failure.

Find the indices of the adjacent vertices of the vertex ip of the triangle start.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_GET_ADJAVERTICESFAST(mesh,ip,start,lispoi,retval)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh
INTEGER(MMG5F_INT), INTENT(IN) :: ip,start
INTEGER(MMG5F_INT), DIMENSION(MMGS_LMAX), INTENT(OUT) :: lispoi
INTEGER(MMG5F_INT), INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 723 of file libmmgs_tools.c.

Here is the caller graph for this function:

◆ MMGS_Get_nonBdyEdge()

int MMGS_Get_nonBdyEdge	(	MMG5_pMesh	mesh,
		MMG5_int *	e0,
		MMG5_int *	e1,
		MMG5_int *	ref,
		MMG5_int	idx
	)

Get vertices and reference of a non-boundary edge.

Parameters

mesh	pointer to the mesh structure.
e0	pointer to the first extremity of the edge (a vertex number).
e1	pointer to the second extremity of the edge (a vertex number).
ref	pointer to the edge reference.
idx	index of the non boundary edge to get (between 1 and the number of edges)

Returns: 0 on failure, 1 otherwise.

This function returns the vertices e0, e1 and reference ref of the non boundary edge idx. An edge is boundary if it is located at the interface of 2 domains with different references, if it belongs to one triangle only or if it is a singular edge (ridge or required).

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_GET_NONBDYEDGE(mesh,e0,e1,ref,idx,retval)
MMG5_DATA_PTR_T,INTENT(INOUT) :: mesh
INTEGER(MMG5F_INT), INTENT(OUT):: e0,e1
INTEGER(MMG5F_INT) :: ref
INTEGER(MMG5F_INT), INTENT(IN) :: idx
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 667 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Get_numberOfNonBdyEdges()

int MMGS_Get_numberOfNonBdyEdges	(	MMG5_pMesh	mesh,
		MMG5_int *	nb_edges
	)

Get the number of non-boundary edges.

Parameters

mesh	pointer to the mesh structure.
the	number of edges pointer to the number of non boundary edges.

Returns: 0 on failure, 1 otherwise.

Get the number of non-boundary edges (for DG methods for example). An edge is boundary if it is located at the interface of 2 domains with different references, if it belongs to one triangle only or if it is a singular edge (ridge or required). Append these edges to the list of edges.

Warning: reallocate the edge array and append the internal edges. This may modify the behaviour of other functions.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_GET_NUMBEROFNONBDYEDGES(mesh,nb_edges,retval)
MMG5_DATA_PTR_T,INTENT(INOUT) :: mesh
INTEGER(MMG5F_INT), INTENT(OUT):: nb_edges
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 571 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_parsar()

int MMGS_parsar	(	int	argc,
		char *	argv[],
		MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pSol	sol
	)

Store command line arguments.

Parameters

argc	number of command line arguments.
argv	command line arguments.
mesh	pointer to the mesh structure.
met	pointer to the sol structure.
sol	pointer to a level-set or displacement

Returns: 1.

Remarks: no matching fortran function.

Definition at line 126 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_Set_constantSize()

int MMGS_Set_constantSize	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Compute a constant size map.

Parameters

mesh	pointer to the mesh structure
met	pointer to the sol structure

Returns: 1 on success

This function computes a constant size map according to mesh->info.hsiz, mesh->info.hmin and mesh->info.hmax. It updates these 3 values if they are not compatible.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_SET_CONSTANTSIZE(mesh,met,retval)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh,met
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 1579 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_setfunc()

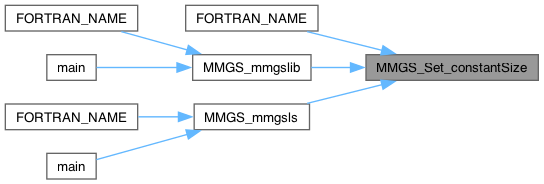
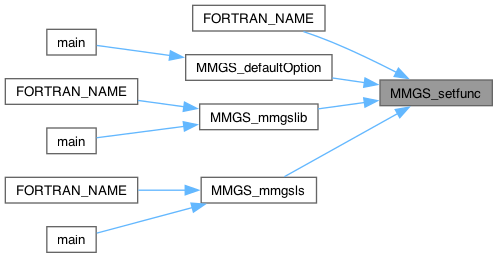
void MMGS_setfunc	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Set function pointers for caltet, lenedg, defsiz and gradsiz.

To associate function pointers without calling MMGS_mmgslib

Parameters

mesh	pointer to the mesh structure (unused).
met	pointer to the sol structure (unused).

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_SETFUNC(mesh,met)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh,met
END SUBROUTINE

Definition at line 43 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_solTruncatureForOptim()

static int MMGS_solTruncatureForOptim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		int	ani
	)

inlinestatic

Parameters

mesh	pointer to the mesh structure.
met	pointer to the solution structure.
ani	1 for aniso metric, 0 for iso one

Returns: 0 if fail, 1 if succeed.

Truncate the metric computed by the DoSol function by hmax and hmin values (if setted by the user). Set hmin and hmax if they are not setted.

Definition at line 810 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_stockOptions()

int MMGS_stockOptions	(	MMG5_pMesh	mesh,
		MMG5_Info *	info
	)

Store the info structure in the mesh structure.

Parameters

mesh	pointer to the mesh structure.
info	pointer to the info structure.

Returns: 1.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_STOCKOPTIONS(mesh,info,retval)
MMG5_DATA_PTR_T, INTENT(INOUT) :: mesh,info
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 552 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_surfopenballRotation()

static int MMGS_surfopenballRotation	(	MMG5_pMesh	mesh,
		MMG5_pPoint	p0,
		MMG5_int	k,
		int	i,
		int	ilist,
		double	r[3][3],
		double *	lispoi,
		double	n[3]
	)

inlinestatic

Parameters

mesh	pointer to the mesh structure.
p0	starting point
k	index of starting element
i	local index of p0 in k
ilist	computed number of tria in the ball of p0
r	rotation that send the normal at p0 onto the z vector
lipoint	rotated ball of point p0
n	normal at point p0

Returns: 1 if success, 0 otherwise.

Compute the rotation matrix that sends the tangent plane at p0 onto z=0 and apply this rotation to the opened ball of p0.

Definition at line 1050 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_unitTensor_2D()

static int MMGS_unitTensor_2D	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int	i,
		MMG5_pPoint	p1,
		double *	m,
		double	isqhmax
	)

inlinestatic

Parameters

mesh	pointer to the mesh
k	index of starting triangle
i	local index of point p1 in k
p1	point on which we want to compute the 3D unit tensor
m	pointer to store computed metric
isqhmax	squared inverse of MMG5_HMAXCOE

Returns: 1 if succeed, 0 if fail.

Compute the 2D unit tensor at point p1, the vertex number i of tetra k : edges of the ball of point are projected onto the tangent plane.

Step 1: compute ball of point

Step 2: Store or compute the suitable normal depending on the type of point we are processing.

Step 3: Rotation of the ball of p0 so lispoi will contain all the points of the ball of p0, rotated so that t_{p_0}S = [z = 0]

Step 4: computation of unit tensor

Definition at line 1148 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_unitTensor_3D()

static int MMGS_unitTensor_3D	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int	i,
		MMG5_pPoint	p1,
		double *	m
	)

inlinestatic

Parameters

mesh	pointer to the mesh
k	index of starting triangle
i	local index of point p1 in k
p1	point on which we want to compute the 3D unit tensor
m	pointer to store computed metric

Returns: 1 if succeed, 0 if the tensor of covariance is non invertible.

Compute the 3D unit tensor at point p1, the vertex number i of tetra k.

Remarks: If all edges starting from p1 belong to the same plane, the tensor of covariance is not invertible and m can't be computed.

Step 1: compute ball of point

Step 2: compute unit tensor

Definition at line 939 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ MMGS_usage()

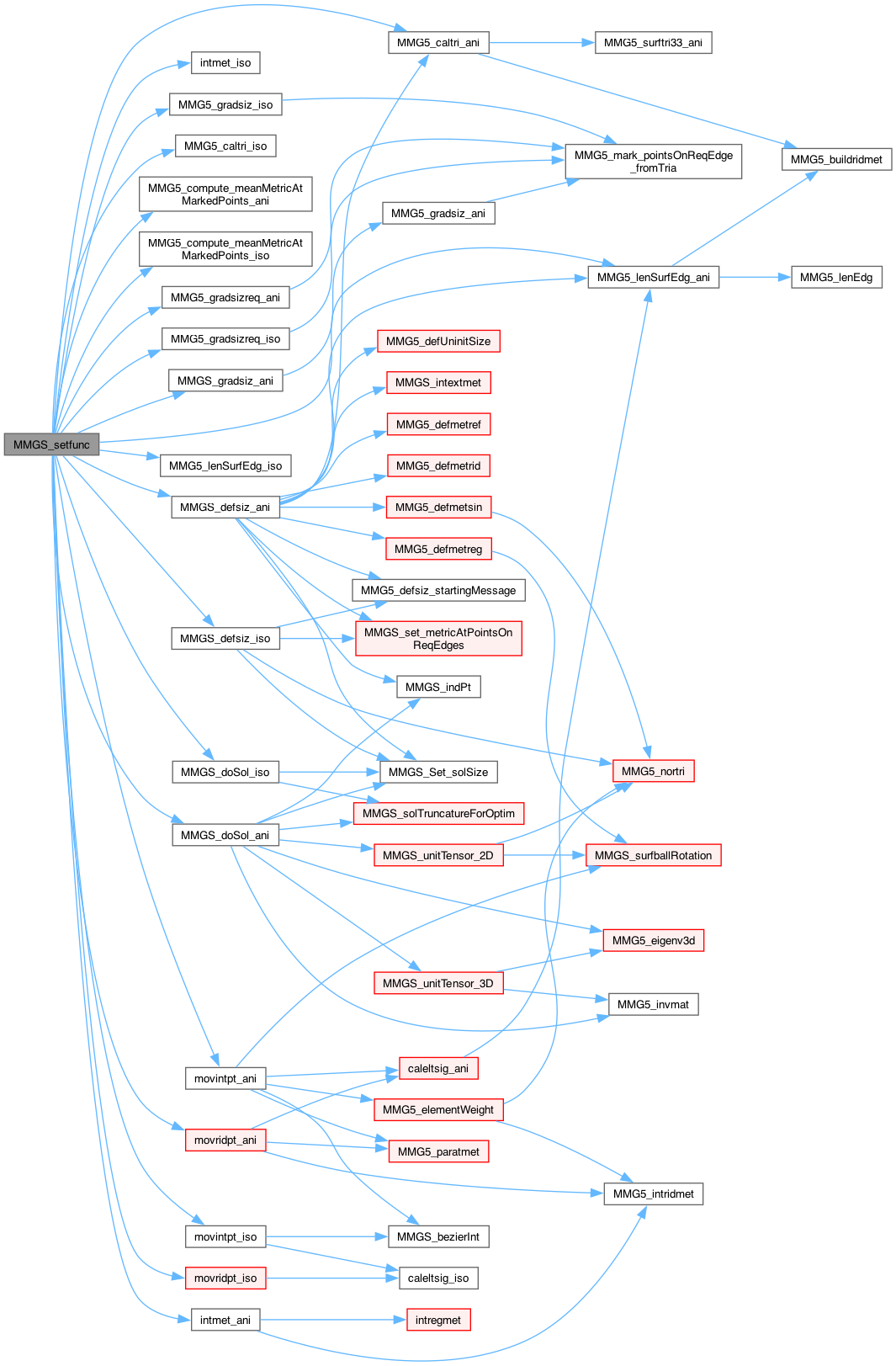
int MMGS_usage ( char * prog )

Print help for mmgs options.

Parameters

prog	pointer to the program name.

Remarks: Fortran interface:

‍ SUBROUTINE MMGS_USAGE(prog,strlen0,retval)
CHARACTER(LEN=*), INTENT(IN) :: prog
INTEGER, INTENT(IN) :: strlen0
INTEGER, INTENT(OUT) :: retval
END SUBROUTINE

Definition at line 83 of file libmmgs_tools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

Functions

Detailed Description

Function Documentation

◆ MMGS_Clean_isoSurf()

◆ MMGS_Compute_eigenv()

◆ MMGS_defaultValues()

◆ MMGS_destockOptions()

◆ MMGS_doSol_ani()

◆ MMGS_doSol_iso()

◆ MMGS_Free_solutions()

◆ MMGS_freeLocalPar()

◆ MMGS_Get_adjaTri()

◆ MMGS_Get_adjaVerticesFast()

◆ MMGS_Get_nonBdyEdge()

◆ MMGS_Get_numberOfNonBdyEdges()

◆ MMGS_parsar()

◆ MMGS_Set_constantSize()

◆ MMGS_setfunc()

◆ MMGS_solTruncatureForOptim()

◆ MMGS_stockOptions()

◆ MMGS_surfopenballRotation()

◆ MMGS_unitTensor_2D()

◆ MMGS_unitTensor_3D()

◆ MMGS_usage()