bezier_3d.c File Reference

Functions for Bezier surface computation. More...

#include "libmmg3d_private.h"

Include dependency graph for bezier_3d.c:

Go to the source code of this file.

Functions
int	MMG5_BezierTgt (double c1[3], double c2[3], double n1[3], double n2[3], double t1[3], double t2[3])
double	MMG5_BezierGeod (double c1[3], double c2[3], double t1[3], double t2[3])
int	MMG5_BezierEdge (MMG5_pMesh mesh, MMG5_int ip0, MMG5_int ip1, double b0[3], double b1[3], int8_t ised, double v[3])
int	MMG5_mmg3dBezierCP (MMG5_pMesh mesh, MMG5_Tria *pt, MMG5_pBezier pb, int8_t ori)
int	MMG3D_bezierInt (MMG5_pBezier pb, double uv[2], double o[3], double no[3], double to[3])

Variables
int8_t	ddb

Detailed Description

Functions for Bezier surface computation.

Author

Charles Dapogny (UPMC)

Cécile Dobrzynski (Bx INP/Inria/UBordeaux)

Pascal Frey (UPMC)

Algiane Froehly (Inria/UBordeaux)

Version

5

Copyright

GNU Lesser General Public License.

Definition in file bezier_3d.c.

Function Documentation

MMG3D_bezierInt()

int MMG3D_bezierInt	(	MMG5_pBezier	pb,
		double	uv[2],
		double	o[3],
		double	no[3],
		double	to[3]
	)

Parameters

pb	pointer to the Bezier structure.
uv	coordinates of the point in the parametric space.
o	computed coordinates of the point in the real space.
no	computed normal.
to	computed tangent.

Returns

1.

Compute o, no and to at \((u,v)\) in Bezier patch.

Definition at line 608 of file bezier_3d.c.

Here is the caller graph for this function:

MMG5_BezierEdge()

int MMG5_BezierEdge ( MMG5_pMesh  mesh, MMG5_int  ip0, MMG5_int  ip1, double  b0[3], double  b1[3], int8_t  ised, double  v[3]  )

inline

Parameters

mesh	pointer to the mesh structure.
ip0	index of the first point of the curve.
ip1	index of the second point of the curve.
b0	the first computed extrapolated control point.
b1	the second computed extrapolated control point.
ised	flag for special edge.
v	direction for normal vectors.

Compute control points associated to the underlying curve to \([p0;p1]\). ised = 1 if \([p0;p1]\) must be considered as a special edge. Provide a direction v which will be considered as reference when dealing with choice of normal vectors.

Definition at line 152 of file bezier_3d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_BezierGeod()

double MMG5_BezierGeod ( double  c1[3], double  c2[3], double  t1[3], double  t2[3]  )

inline

Parameters

c1	coordinates of the first point of the curve.
c2	coordinates of the second point of the curve.
t1	normal at the first point of the curve.
t2	normal at the second point of the curve.

Returns

The parameter value.

Compute value of the parameter that makes the underlying Bezier curve with 'constant speed'

Definition at line 111 of file bezier_3d.c.

Here is the caller graph for this function:

MMG5_BezierTgt()

int MMG5_BezierTgt ( double  c1[3], double  c2[3], double  n1[3], double  n2[3], double  t1[3], double  t2[3]  )

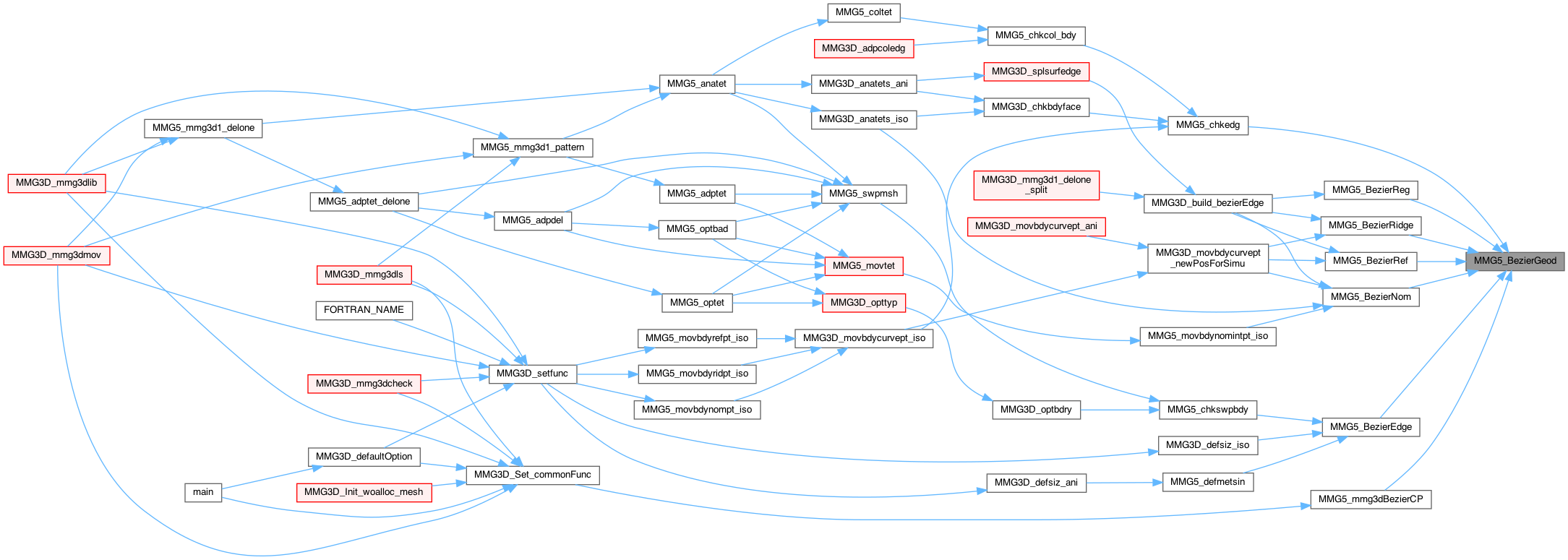
inline

Parameters

c1	coordinates of the first point of the curve.
c2	coordinates of the second point of the curve.
n1	normal at the first point of the curve.
n2	normal at the second point of the curve.
t1	computed normal at the first point of the curve.
t2	computed normal at the second point of the curve.

Returns

0 if failed, 1 otherwise.

Compute tangent to geometric support curve passing through c1,c2, with normals n1,n2

Definition at line 53 of file bezier_3d.c.

Here is the caller graph for this function:

MMG5_mmg3dBezierCP()

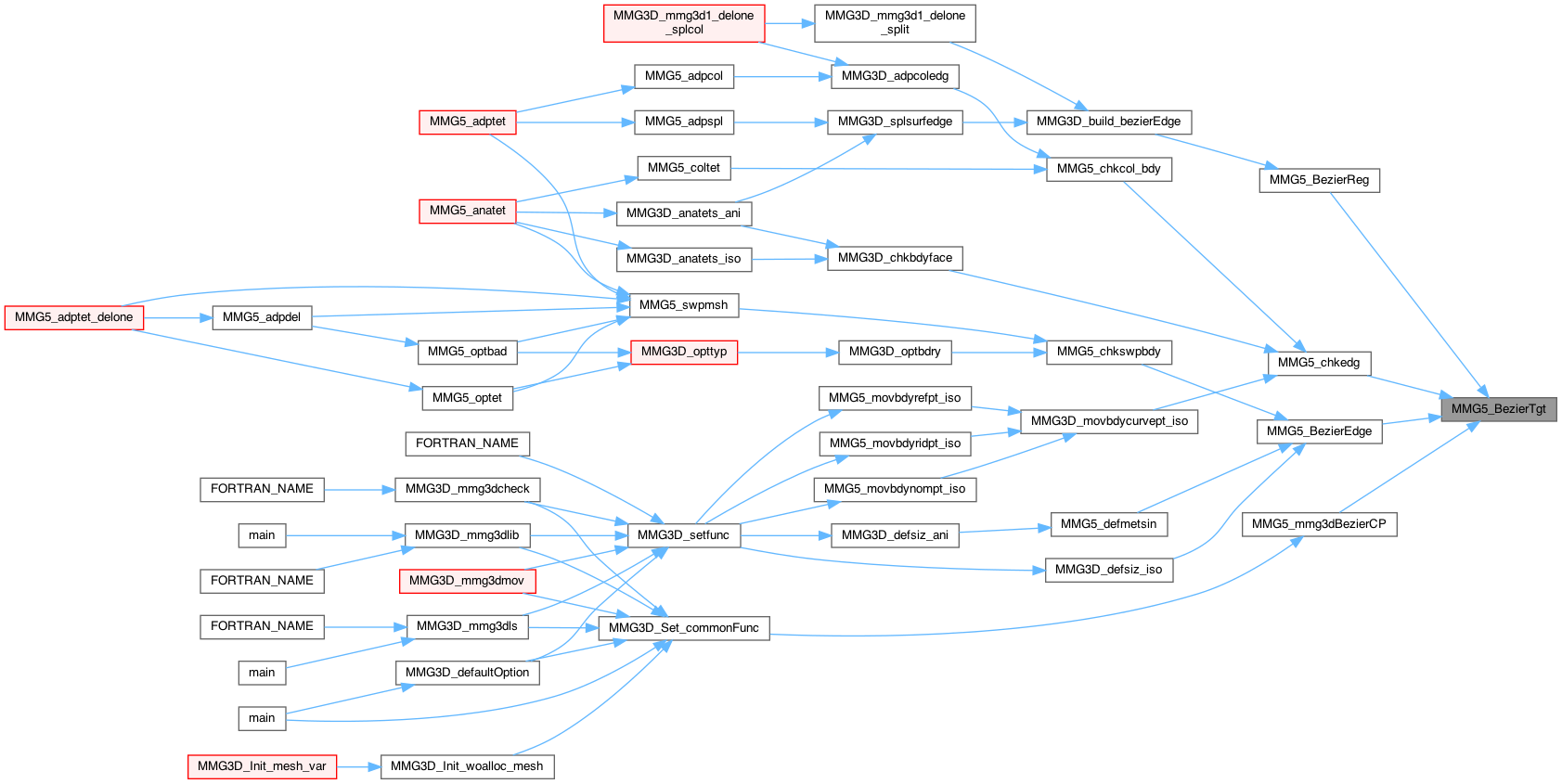
int MMG5_mmg3dBezierCP	(	MMG5_pMesh	mesh,
		MMG5_Tria *	pt,
		MMG5_pBezier	pb,
		int8_t	ori
	)

Parameters

mesh	pointer to the mesh structure.
pt	pointer to the triangle structure.
pb	pointer to the computed Bezier structure.
ori	triangle orientation.

Returns

1.

Compute Bezier control points on triangle pt (cf. [4])

Todo:

merge with the MMG5_mmgsBezierCP function and remove the pointer toward this functions.

Remarks

• prior to commit f57b861966: we were comparing absolute values of normals projection (guessing that normals can be bad oriented). In this case, we can choose the wrong normal (normal at point related to other portion of surface) when the ridge angle is almost closed (smallest than 90°) because projection of normal at first triangle and normal at second triangle (or normal at point related to second surface) tends to -1;
• the following assert on the positivity of at least one of the projections may fail but I think that it is not a normal behaviour: it means that the surface approximation has degenerated. See issue #167

Orientation of the normals at non-manifold points

Definition at line 326 of file bezier_3d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

ddb

int8_t ddb

extern

Definition at line 42 of file mmg3d1_delone.c.