anisosiz_2d.c File Reference

Interpolation of metrics. More...

#include "libmmg2d_private.h"
#include "libmmg2d.h"
#include "mmg2dexterns_private.h"

Include dependency graph for anisosiz_2d.c:

Go to the source code of this file.

Functions
int	MMG2D_defaultmet_2d (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i)
int	MMG2D_defmetbdy_2d (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t i)
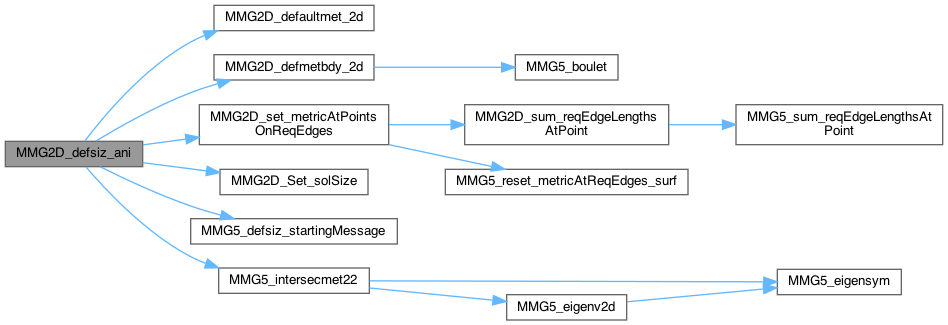
int	MMG2D_defsiz_ani (MMG5_pMesh mesh, MMG5_pSol met)
static void	MMG2D_gradEigenv (double dm[2], double dn[2], double difsiz, int8_t dir, int8_t *ier)
MMG5_int	MMG2D_grad2met_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_pTria pt, MMG5_int np1, MMG5_int np2)
int	MMG2D_grad2metreq_ani (MMG5_pMesh mesh, MMG5_pSol met, MMG5_pTria pt, MMG5_int npmaster, MMG5_int npslave)

Detailed Description

Interpolation of metrics.

Author

Charles Dapogny (UPMC)

Cécile Dobrzynski (Bx INP/Inria/UBordeaux)

Pascal Frey (UPMC)

Algiane Froehly (Inria/UBordeaux)

Version

5

Date

01 2014

Copyright

GNU Lesser General Public License.

Definition in file anisosiz_2d.c.

Function Documentation

MMG2D_defaultmet_2d()

int MMG2D_defaultmet_2d	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
k	elt index
i	vertex index in triangle k

Returns

0 if fail, 1 if success

Impose default metric (isotropic, with size hmax) at vertex i in triangle k (don't take into account the local parameters). Set the point flag to 1 to be able to truncate it with the local params later.

Definition at line 51 of file anisosiz_2d.c.

Here is the caller graph for this function:

MMG2D_defmetbdy_2d()

int MMG2D_defmetbdy_2d	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int8_t	i
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
k	index of the tria in which we work
i	index of the point on which we want to compute the metric

Returns

1 if success, 0 if fail

Calculate anisotropic metric tensor at (boundary) vertex i in triangle k on account of geometric approximation of the corresponding curve (taking into account the local parameters). Set the point flag to 2 to ignore it whem imposing the local parameters later.

Definition at line 86 of file anisosiz_2d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG2D_defsiz_ani()

int MMG2D_defsiz_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric

Returns

0 if fail, 1 if success

Definition of an anisotropic metric tensor field based on the geometry of the domain; this tensor field is intersected by a user-defined tensor field

Step 1: Set metric at points belonging to a required edge: compute the metric as the mean of the length of the required eges passing through the point

For points with flag 1 (metrec computed by defaultmet_2d), truncation by the local parameters

Definition at line 363 of file anisosiz_2d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG2D_grad2met_ani()

MMG5_int MMG2D_grad2met_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pTria	pt,
		MMG5_int	np1,
		MMG5_int	np2
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
pt	pointer to the processed triangle.
np1	first edge extremity (global index)
np2	second edge extremity (global index)

Returns

0 if fail or we don't need to modify the sizes. ier, where (ier & 1) if metric of ip1 is altered, and (ier & 2) if metric of ip2 is altered.

Perform simultaneous reduction of metrics at ip1 points and ip2, and truncate characteristic sizes so that the difference between two corresponding sizes respect the maximal gradation.

Ref : https://www.rocq.inria.fr/gamma/Frederic.Alauzet/cours/cea2010_V2.pdf

Definition at line 537 of file anisosiz_2d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG2D_grad2metreq_ani()

int MMG2D_grad2metreq_ani	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_pTria	pt,
		MMG5_int	npmaster,
		MMG5_int	npslave
	)

Parameters

mesh	pointer to the mesh
met	pointer to the metric
pt	pointer to the processed tria.
npmaster	edge extremity that cannot be modified
npslave	edge extremity to modify to respect the gradation.

Returns

0 if fail or we don't need to update the size of ipslave, 1 if its size has been updated.

Perform simultaneous reduction of metrics at npmaster points and npslave, and modify the characteristic size of npslave so that the difference between the two sizes respect the maximal gradation

Ref : https://www.rocq.inria.fr/gamma/Frederic.Alauzet/cours/cea2010_V2.pdf

Definition at line 600 of file anisosiz_2d.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG2D_gradEigenv()

static void MMG2D_gradEigenv ( double  dm[2], double  dn[2], double  difsiz, int8_t  dir, int8_t *  ier  )

inlinestatic

Parameters

dm	eigenvalues of the first matrix
dn	eigenvalues of the second matrix
difsiz	maximal size gap authorized by the gradation.
dir	direction in which the sizes are graded.
ier	flag of the modified eigenvalue: (ier & 1) if dm is altered, and (ier & 2) if dn is altered.

Gradation of sizes = 1/sqrt(eigenv of the tensors) in the idir direction.

Definition at line 501 of file anisosiz_2d.c.

Here is the caller graph for this function: