Mmg
Simplicial remeshers (mesh adaptation, isovalue discretization, lagrangian movement)
Functions
analys_3d.c File Reference

Mesh analysis. More...

#include "libmmg3d.h"
#include "libmmg3d_private.h"
Include dependency graph for analys_3d.c:

Go to the source code of this file.

Functions

void MMG3D_set_reqBoundaries (MMG5_pMesh mesh)
 
int MMG5_setadj (MMG5_pMesh mesh)
 
int MMG5_setdhd (MMG5_pMesh mesh)
 
int MMG5_chkVertexConnectedDomains (MMG5_pMesh mesh)
 
int MMG5_singul (MMG5_pMesh mesh)
 
int MMG5_norver (MMG5_pMesh mesh)
 
static int MMG3D_dichotomytria (MMG5_pMesh mesh, MMG5_pTria pt, MMG5_int k, double *c, double *n)
 
static int MMG3D_dichotomytetra (MMG5_pMesh mesh, MMG5_int *v, MMG5_int k, double *c)
 
int MMG3D_regver (MMG5_pMesh mesh)
 
int MMG3D_nmgeom (MMG5_pMesh mesh)
 
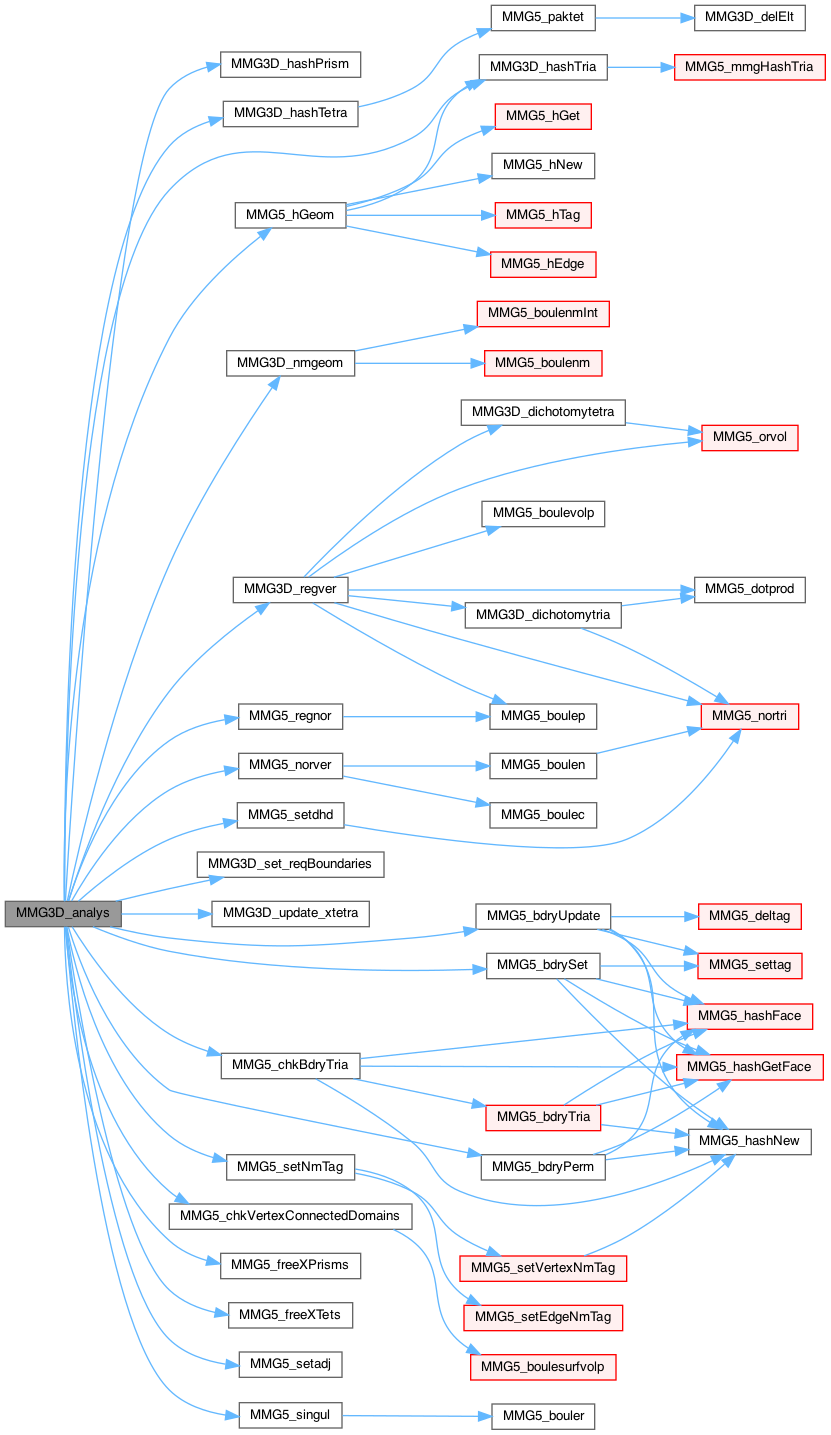
int MMG3D_analys (MMG5_pMesh mesh)
 

Detailed Description

Mesh analysis.

Author
Charles Dapogny (UPMC)
Cécile Dobrzynski (Bx INP/Inria/UBordeaux)
Pascal Frey (UPMC)
Algiane Froehly (Inria/UBordeaux)
Version
5
Copyright
GNU Lesser General Public License.
Todo:
doxygen documentation.

Definition in file analys_3d.c.

Function Documentation

◆ MMG3D_analys()

int MMG3D_analys ( MMG5_pMesh  mesh)
Parameters
meshpointer toward mesh
Returns
1 if successful, 0 if fail

preprocessing stage: mesh analysis.

At the end of this function:

  1. triangles have been deleted and stored in xtetra;
  2. Boundary point have been analyzed and associated to xpoints (if needed). If computed tangent is stored in ppt->n and normals in pxp->n1 and pxp->n2. Following list summerizes computed (and not computed) data depending on point type:
    • Corner point (MG_CRN): no computation (and no xpoint);
    • Required points have different treatment depending if they are along a 'regular' surf point, along an internal or external non-manifold edge, along a non connex mesh part(so they may have a xpoint, a tangent and a normal or not) but their normal is not used during remeshing. See comments in MMG3D_nmgeom
    • Reference point (MG_REF): xpoint, tangent, 1 normal;
    • Ridge point (MG_GEO): xp, tangent,2 normals;
    • Non-manifold point (MG_NOM): xp, tangent, no normal if internal, 1 normal if external
    • Open boundary points (MG_OPNBDY) are treated as nm points.

— stage 1: data structures for surface

— stage 2: surface analysis

Definition at line 1324 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG3D_dichotomytetra()

static int MMG3D_dichotomytetra ( MMG5_pMesh  mesh,
MMG5_int *  v,
MMG5_int  k,
double *  c 
)
inlinestatic
Parameters
meshpointer towards the mesh
vlist of vertices of current tetrahedron
knumber of current point
cinput : newly computed coordinates (giving negative area), output : coordinates after dichotomy
Returns
0 if fail, 1 if success

In coordinate regularization, performs a dichotomy between previous point / and newly computed point in the case of negative volume

Definition at line 895 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG3D_dichotomytria()

static int MMG3D_dichotomytria ( MMG5_pMesh  mesh,
MMG5_pTria  pt,
MMG5_int  k,
double *  c,
double *  n 
)
inlinestatic
Parameters
meshpointer towards the mesh
ptpointer towards current triangle
knumber of current point
cnewly computed coordinates (giving negative area)
nnormal of triangle before regularization
Returns
0 if fail, 1 if success

In coordinate regularization, performs a dichotomy between previous point / and newly computed point in the case of negative area of a triangle

Definition at line 828 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG3D_nmgeom()

int MMG3D_nmgeom ( MMG5_pMesh  mesh)
Parameters
meshpointer toward the mesh
Returns
0 if fail, 1 otherwise

Define continuous geometric support at non manifold vertices, using volume information.

Following list summerizes computed data depending on point type:

  • Non-manifold external point along connex mesh part (MG_NOM): xp, tangent, normal n1, nnor=0
  • Non-manifold external point along edge or point connected mesh part (MG_NOM): no xp,no tangent,no normal,nnor=0
  • Non-manifold not required internal point (MG_NOM+MG_REQ): xp, tangent, no normal, nnor=1.
  • Non-manifold required internal point (MG_NOM+MG_REQ): no xp, no tangent, no normal, nnor=1.
  • Non-manifold open-boundary (MG_OPNBDY) edges are treated like others:
    • if we are along a "truly" open boundary, it is an internal nm edge so we don't have any normal;
    • if the edge is marked as open while being only non-manifold, we may compute a normal (along an external boundary) or not (along an internal one).
  • We don't compute anything along corner points.

Definition at line 1198 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG3D_regver()

int MMG3D_regver ( MMG5_pMesh  mesh)
Parameters
meshpointer toward a MMG5 mesh structure.
Returns
0 if fail, 1 otherwise.

Regularization procedure for vertices coordinates, dual Laplacian in 3D

Definition at line 956 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG3D_set_reqBoundaries()

void MMG3D_set_reqBoundaries ( MMG5_pMesh  mesh)
Parameters
meshpointer towarad the mesh structure.

Set all boundary triangles to required and add a tag to detect that they are not realy required.

Definition at line 46 of file analys_3d.c.

Here is the caller graph for this function:

◆ MMG5_chkVertexConnectedDomains()

int MMG5_chkVertexConnectedDomains ( MMG5_pMesh  mesh)
Parameters
meshpointer toward the mesh structure.
Returns
1.

check subdomains connected by a vertex and mark these vertex as CRN and REQ.

Definition at line 471 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG5_norver()

int MMG5_norver ( MMG5_pMesh  mesh)
Parameters
meshpointer toward mesh
Returns
1 if successful, 0 if failed

Compute normals at C1 vertices, for C0: tangents.

Following list summerizes computed (and not computed) data depending on point type:

  • Corner point (MG_CRN): nothing (and no xpoint);
  • Reference point (MG_REF): xp, tangent (ppt->n), 1 normal (pxp->n1);
  • Ridge point (MG_GEO): xp, tangent,2 normals (pxp->n1 and n2);
  • Non-manifold point (MG_NOM) are not filled here but in nmgeom function
  • Open boundary points (MG_OPNBDY) are non-manifold so they are filled in nmgeom too.
  • Required points are analyzed using their other flags (so they may have an xpoint and a normal) but their normal is not used during remeshing.

Normals at regular boundary points can be provided by users but are ignored along featured edges.

recomputation of normals only if mesh->xpoint has been freed

Step 1: identify boundary points

input normals are ignored along all type of featured edges (ref, geo, nom) but it is possible to implement their taking into account along non-ridges reference edges and external non-manifold ones.

Step 2: Allocate memory to store normals for boundary points

Step 3: compute normals + tangents

At C1 point

along ridge-curve

Along ridge: compute tangent as intersection of n1 + n2

Definition at line 638 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG5_setadj()

int MMG5_setadj ( MMG5_pMesh  mesh)
Parameters
meshpointer towarad the mesh structure.
Returns
0 if fail, 1 otherwise.

topology: set tria adjacency, detect Moebius, flip faces, count connected comp.

Remarks
: as all triangles are mesh boundaries, we do not need to mark their adges as MG_BDY so the MG_BDY tag may be used inside geometrical triangles (external non-parallel, or internal parallel) to tag edges on the intersection with purely parallel (non-geometrical) triangles. The MG_PARBDYBDY tag is also added, as it does not have a supporting triangle to inherit this tag from.
REQ, NOSURF, etc... tags are added only inside xtetra.
In openbdy mode, all non-manifold edges are marked as opnbdy.

Definition at line 108 of file analys_3d.c.

Here is the caller graph for this function:

◆ MMG5_setdhd()

int MMG5_setdhd ( MMG5_pMesh  mesh)

check for ridges: dihedral angle

Step 1: check input ridges provided by the user to remove those ones between triangles belonging to the same plane. This step has to be done prior the next one because we want to remove the MG_GEO tag transfered from ridges that we delete toward vertices by MMG5_setadj but we want to preserve the MG_GEO tags at vertices of ridges that will be added by the next step.

Step 2: check ref and angle with neighbour to update ref tags and ridge ones

Definition at line 310 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ MMG5_singul()

int MMG5_singul ( MMG5_pMesh  mesh)

check for singularities

Definition at line 544 of file analys_3d.c.

Here is the call graph for this function:
Here is the caller graph for this function:
Generated on Tue Dec 13 2022 00:20:02 for Mmg by doxygen 1.9.5