split_s.c File Reference

Functions to create new points. More...

#include "libmmgs_private.h"
#include "mmgsexterns_private.h"
#include "mmgexterns_private.h"

Include dependency graph for split_s.c:

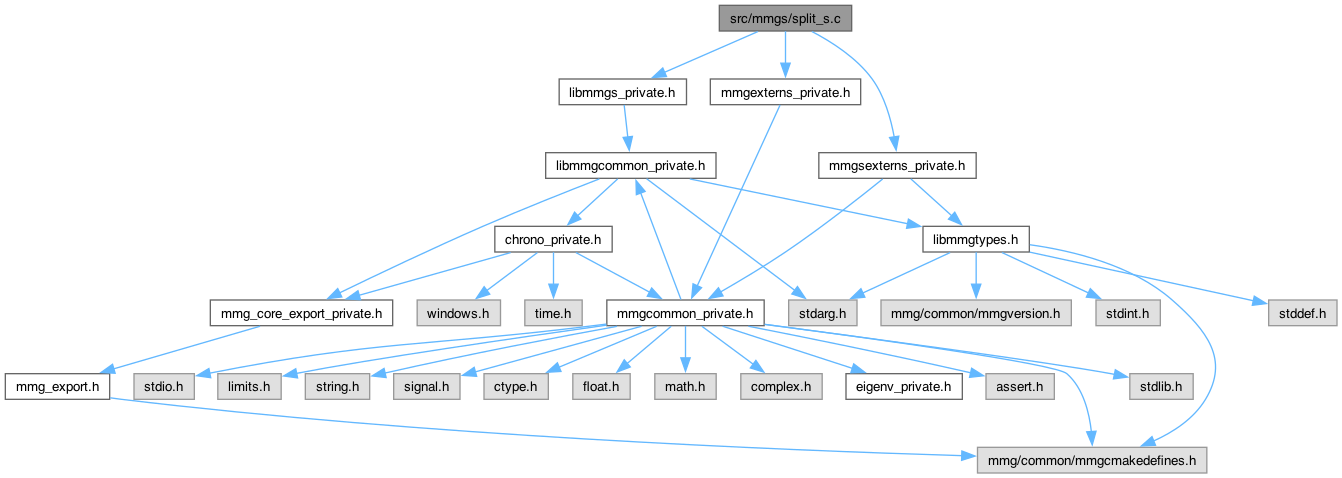
Go to the source code of this file.

Functions
int	MMGS_split1_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int *vx)
int	MMGS_split1 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int *vx)
int	MMGS_simbulgept (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int i, MMG5_int ip)
int	split1b (MMG5_pMesh mesh, MMG5_int k, int8_t i, MMG5_int ip)
int	MMG5_split2_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)
int	MMGS_split2 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)
int	MMGS_split3_sim (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)
int	MMGS_split3 (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, MMG5_int *vx)

Detailed Description

Functions to create new points.

Author

Charles Dapogny (UPMC

Cécile Dobrzynski (Bx INP/Inria/UBordeaux

Pascal Frey (UPMC

Algiane Froehly (Inria/UBordeaux

Version

5

Copyright

GNU Lesser General Public License.

Definition in file split_s.c.

Function Documentation

MMG5_split2_sim()

int MMG5_split2_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns

0 if split leads to invalid element, else 1.

Simulate the splitting of element k along the 2 edges i1 and i2. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 383 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMGS_simbulgept()

int MMGS_simbulgept	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int	ip
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of the starting triangle.
i	local index of the edge to split in k.
ip	index of the point that we try to create.

Returns

0 if final position is invalid or if computation of bezier patch fails, 1 if all checks are ok.

Simulate the creation of the point ip, to be inserted at an edge. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Remarks

Don't work for non-manifold edge.

Definition at line 162 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMGS_split1()

int MMGS_split1	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
i	index of edge to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns

1 if success, 0 if fail.

Split element k along edge i.

Definition at line 109 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMGS_split1_sim()

int MMGS_split1_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		int	i,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
i	index of edge to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.
k	index of element to split.

Returns

0 if split leads to invalid element, else 1.

Simulate the splitting of element k along edge i. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 52 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMGS_split2()

int MMGS_split2	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns

1 if success, 0 if fail.

Split element k along the 2 edges i1 and i2.

Definition at line 459 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMGS_split3()

int MMGS_split3	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns

1 if success, 0 if fail.

Split element k along the 3 edges

Definition at line 620 of file split_s.c.

Here is the call graph for this function:

MMGS_split3_sim()

int MMGS_split3_sim	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	k,
		MMG5_int *	vx
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
k	index of element to split.
vx	\(vx[i]\) is the index of the point to add on the edge i.

Returns

0 if split leads to invalid element, else 1.

Simulate the splitting of element k along the 3 edges. Check that the new triangles are not empty (otherwise we can create a 0 surface triangle).

Definition at line 532 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function:

split1b()

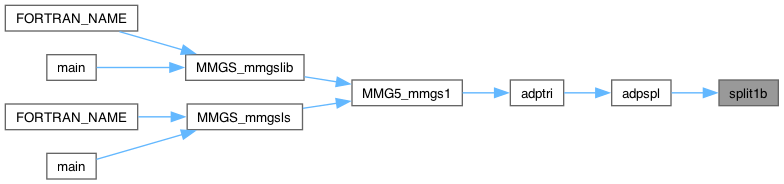
int split1b	(	MMG5_pMesh	mesh,
		MMG5_int	k,
		int8_t	i,
		MMG5_int	ip
	)

Parameters

mesh	pointer to the mesh structure.
k	index of element to split.
i	index of edge to split.
ip	index of the new point.

Returns

0 if lack of memory, 1 otherwise.

Split element k along edge i, inserting point ip and updating the adjacency relations.

Remarks

do not call this function in non-manifold case

Definition at line 283 of file split_s.c.

Here is the call graph for this function:

Here is the caller graph for this function: