mettools.c File Reference

Metric tools for the mmg applications. More...

#include "mmgcommon_private.h"
#include "inlined_functions_private.h"

Include dependency graph for mettools.c:

Go to the source code of this file.

Functions
static void	MMG5_eigenvmat_buildsym (MMG5_pMesh mesh, int8_t dim, double m[], double lambda[], double v[])
static void	MMG5_eigenvmat_buildnonsym (MMG5_pMesh mesh, int8_t dim, double m[], double lambda[], double v[], double iv[])
int	MMG5_eigenvmatsym2d (MMG5_pMesh mesh, double m[], double lambda[], double v[][2])
int	MMG5_eigenvmatsym3d (MMG5_pMesh mesh, double m[], double lambda[], double v[][3])
int	MMG5_eigenvmatnonsym2d (MMG5_pMesh mesh, double m[], double lambda[], double v[][2])
int	MMG5_eigenvmatnonsym3d (MMG5_pMesh mesh, double m[], double lambda[], double v[][3])
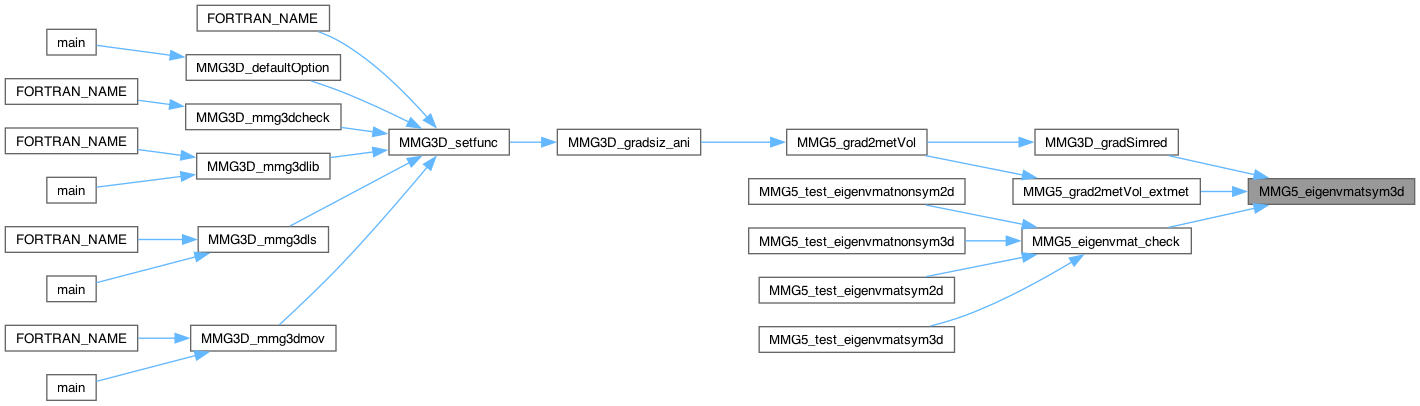
int	MMG5_eigenvmat_check (MMG5_pMesh mesh, int8_t dim, int8_t symmat, double m[], double mnew[])
void	MMG5_sort_eigenv (int8_t dim, double *lambda, double *vp, double *swap, int8_t *perm)
int	MMG5_test_eigenvmatsym2d (MMG5_pMesh mesh, double *mex, double lambdaex[], double vpex[][2])
int	MMG5_test_eigenvmatnonsym2d (MMG5_pMesh mesh, double *mex, double lambdaex[], double vpex[][2], double ivpex[][2])
int	MMG5_test_eigenvmatsym3d (MMG5_pMesh mesh, double *mex, double lambdaex[], double vpex[][3])
int	MMG5_test_eigenvmatnonsym3d (MMG5_pMesh mesh, double *mex, double lambdaex[], double vpex[][3], double ivpex[][3])
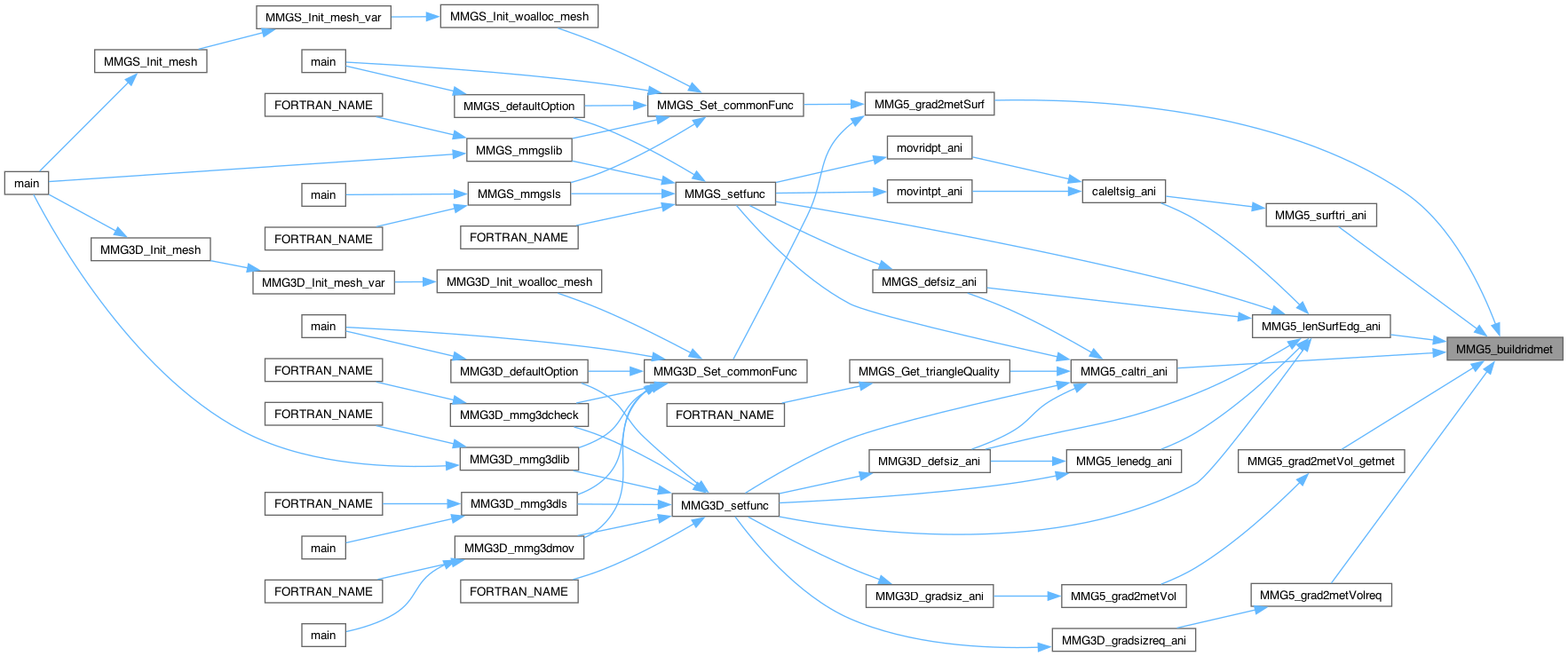
int	MMG5_buildridmetfic (MMG5_pMesh mesh, double t[3], double n[3], double dtan, double dv, double dn, double m[6])
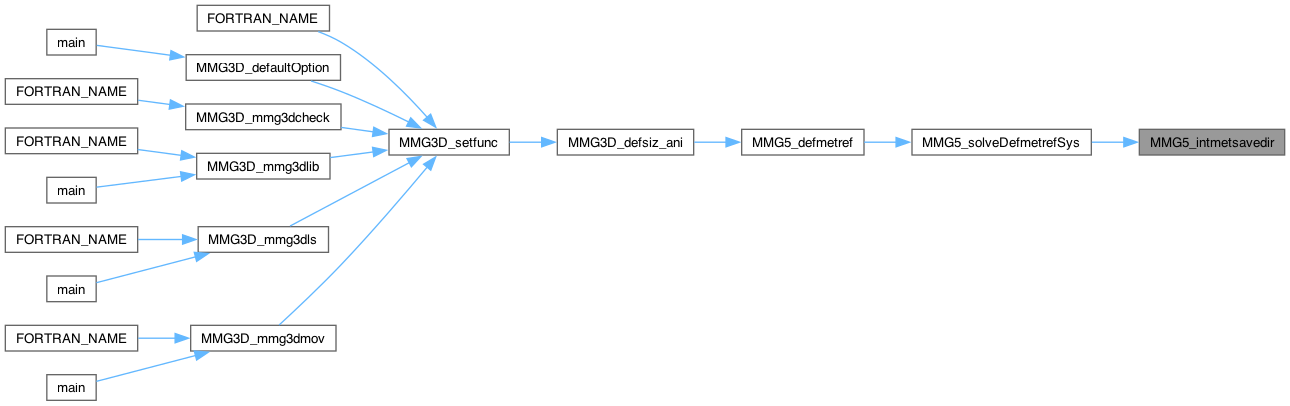
int	MMG5_intmetsavedir (MMG5_pMesh mesh, double *m, double *n, double *mr)
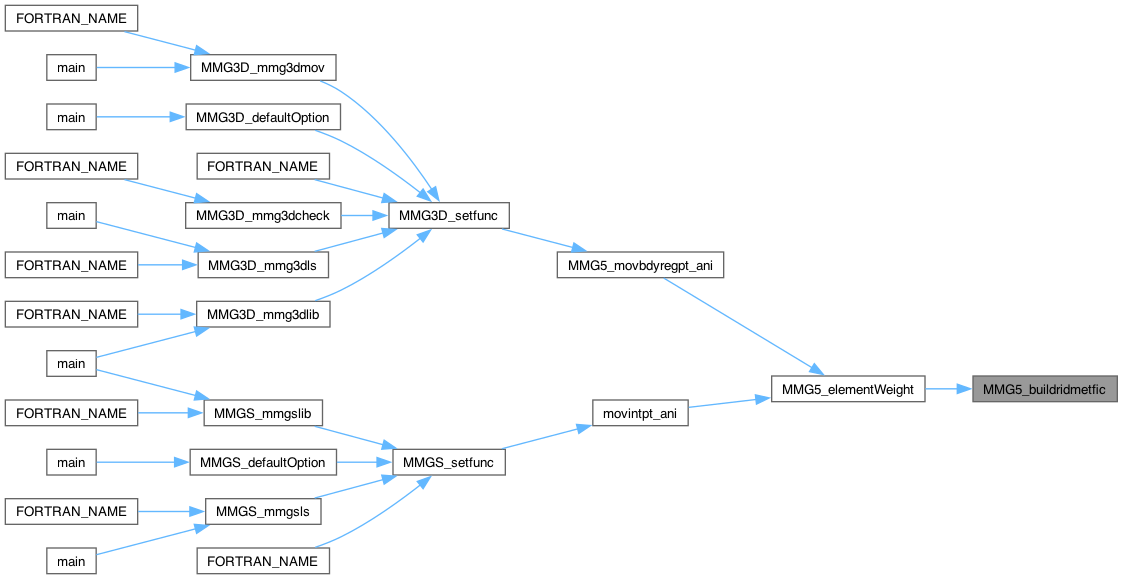
int	MMG5_buildridmet (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int np0, double ux, double uy, double uz, double mr[6], double r[3][3])
int	MMG5_buildridmetnor (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int np0, double nt[3], double mr[6], double r[3][3])
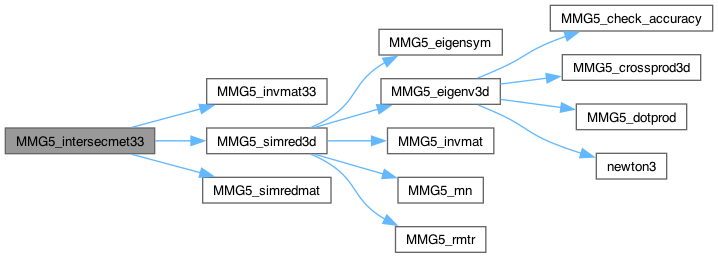
int	MMG5_intersecmet22 (MMG5_pMesh mesh, double *m, double *n, double *mr)
int	MMG5_intersecmet33 (MMG5_pMesh mesh, double *m, double *n, double *mr)
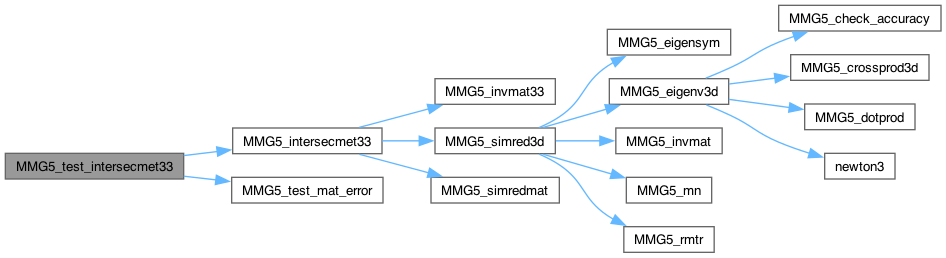
int	MMG5_test_intersecmet22 (MMG5_pMesh mesh)
int	MMG5_test_intersecmet33 (MMG5_pMesh mesh)
int	MMG5_mmgIntextmet (MMG5_pMesh mesh, MMG5_pSol met, MMG5_int np, double me[6], double n[3])
int	MMG5_paratmet (double c0[3], double n0[3], double m[6], double c1[3], double n1[3], double mt[6])

Detailed Description

Metric tools for the mmg applications.

Author

Charles Dapogny (UPMC)

Cécile Dobrzynski (Bx INP/Inria/UBordeaux)

Pascal Frey (UPMC)

Algiane Froehly (Inria/UBordeaux)

Version

5

Copyright

GNU Lesser General Public License.

Definition in file mettools.c.

Function Documentation

MMG5_buildridmet()

int MMG5_buildridmet	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	np0,
		double	ux,
		double	uy,
		double	uz,
		double	mr[6],
		double	r[3][3]
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the sol structure.
np0	index of edge's extremity.
ux	distance \([p0;p1]\) along x axis.
uy	distance \([p0;p1]\) along y axis.
uz	distance \([p0;p1]\) along z axis.
mr	computed metric tensor.
r	basis in which the metric is diagona

Returns

1 if success

Build metric tensor at ridge point p0, when computations with respect to p1 are to be held. Store the basis vectors in r.

Remarks

ALGIANE: a mettre à plat : si p0-p1 est une ridge, on peut reconstruire la mauvaise métrique non? Est-ce qu'il ne vaut mieux pas passer la normale au triangle d'où l'on vient en argument pour le choix de la métrique à reconstruire si c'est possible(quand on vient de grad2metSurfreq)?

Definition at line 676 of file mettools.c.

Here is the caller graph for this function:

MMG5_buildridmetfic()

int MMG5_buildridmetfic ( MMG5_pMesh  mesh, double  t[3], double  n[3], double  dtan, double  dv, double  dn, double  m[6]  )

inline

Parameters

mesh	pointer to the mesh structure.
t	tangent at the ridge point.
n	normal at the ridge point.
dtan	metric size along the tangent direction.
dv	metric size along the \(t^{}n\) direction.
dn	metric size along the normal direction.
m	computed metric at the ridge point.

Returns

1

Build metric tensor at a fictitious ridge point, whose normal and tangent are provided.

Definition at line 601 of file mettools.c.

Here is the caller graph for this function:

MMG5_buildridmetnor()

int MMG5_buildridmetnor	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	np0,
		double	nt[3],
		double	mr[6],
		double	r[3][3]
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the sol structure.
np0	index of edge's extremity.
nt	normal direction at the ridge point.
mr	computed metric tensor.
r	basis in which the metric is diagonal

Returns

0 if fail, 1 if the metric is build with respect to n1, 2 if it is build with respect to n2.

Build metric tensor at ridge point p0, when the 'good' normal direction is given by nt and store the basis vectors in r.

Definition at line 751 of file mettools.c.

Here is the caller graph for this function:

MMG5_eigenvmat_buildnonsym()

static void MMG5_eigenvmat_buildnonsym ( MMG5_pMesh  mesh, int8_t  dim, double  m[], double  lambda[], double  v[], double  iv[]  )

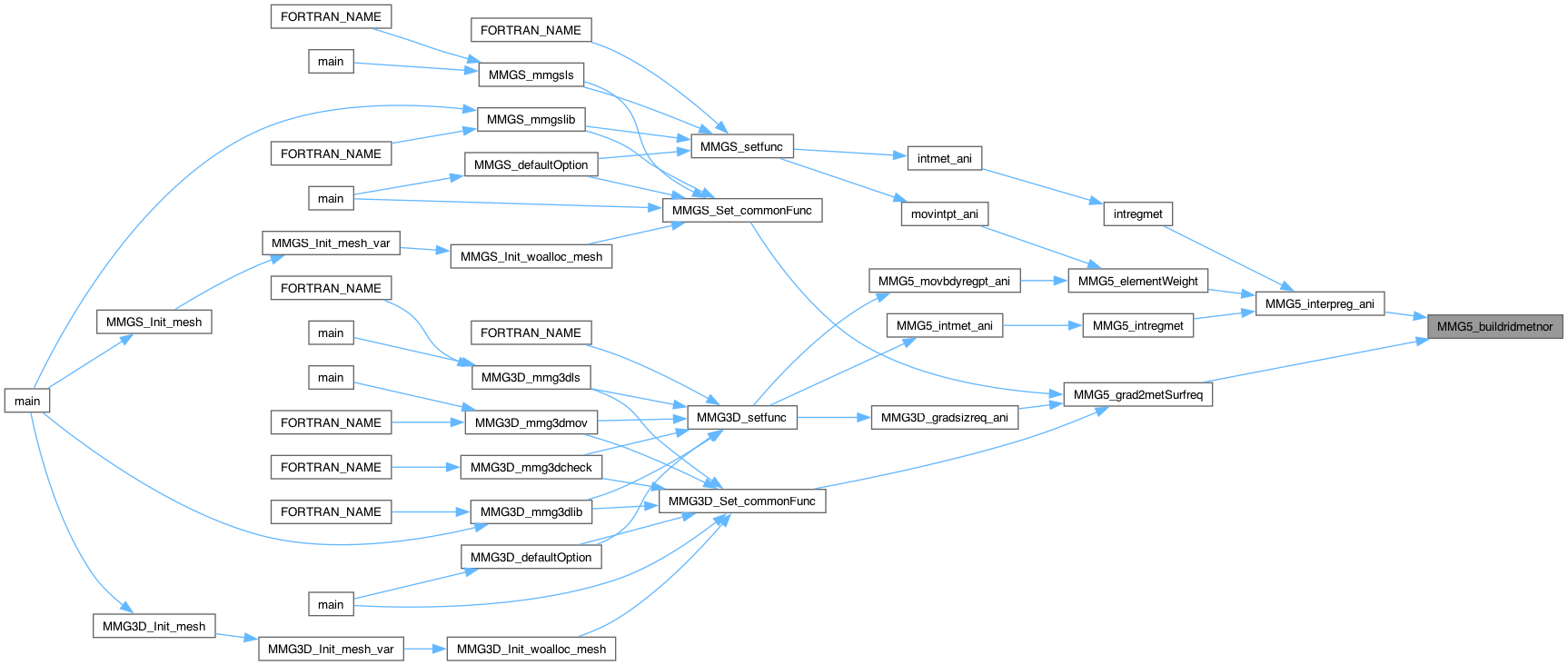
inlinestatic

Parameters

mesh	pointer to the mesh structure.
m	matrix array.
dim	matrix size.
lambda	eigenvalues array.
v	double array of right eigenvectors.
iv	double array of left eigenvectors.

Returns

1 if success, 0 if failure.

Recompose a generic-size non-symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 100 of file mettools.c.

Here is the caller graph for this function:

MMG5_eigenvmat_buildsym()

static void MMG5_eigenvmat_buildsym ( MMG5_pMesh  mesh, int8_t  dim, double  m[], double  lambda[], double  v[]  )

inlinestatic

Parameters

mesh	pointer to the mesh structure.
dim	matrix size.
m	matrix array.
lambda	eigenvalues array.
v	array of eigenvectors.

Recompose a generic-size symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 52 of file mettools.c.

Here is the caller graph for this function:

MMG5_eigenvmat_check()

int MMG5_eigenvmat_check	(	MMG5_pMesh	mesh,
		int8_t	dim,
		int8_t	symmat,
		double	m[],
		double	mnew[]
	)

Parameters

mesh	pointer to the mesh structure.
dim	matrix size.
symmat	integer flag (1 if the matrix is symmetric, 0 otherwise).
m	input matrix array. <param mnew output matrix array.

Returns

1 if success, 0 if failure.

Check the recomposition of a matrix from its numerical eigenvalue decomposition.

Definition at line 233 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_eigenvmatnonsym2d()

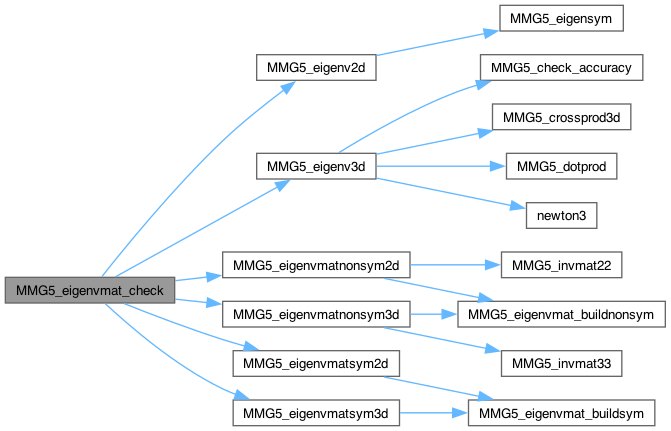
int MMG5_eigenvmatnonsym2d	(	MMG5_pMesh	mesh,
		double	m[],
		double	lambda[],
		double	v[][2]
	)

Parameters

mesh	pointer to the mesh structure.
m	matrix array.
lambda	eigenvalues array.
v	double array of eigenvectors.

Returns

1 if success, 0 if failure.

Recompose a 2x2 non-symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 184 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_eigenvmatnonsym3d()

int MMG5_eigenvmatnonsym3d	(	MMG5_pMesh	mesh,
		double	m[],
		double	lambda[],
		double	v[][3]
	)

Parameters

mesh	pointer to the mesh structure.
m	matrix array.
lambda	eigenvalues array.
v	double array of eigenvectors.

Returns

1 if success, 0 if failure.

Recompose a 3x3 non-symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 209 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_eigenvmatsym2d()

int MMG5_eigenvmatsym2d	(	MMG5_pMesh	mesh,
		double	m[],
		double	lambda[],
		double	v[][2]
	)

Parameters

mesh	pointer to the mesh structure.
m	matrix array.
lambda	eigenvalues array.
v	double array of eigenvectors.

Returns

1 if success, 0 if failure.

Recompose a 2x2 symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 144 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_eigenvmatsym3d()

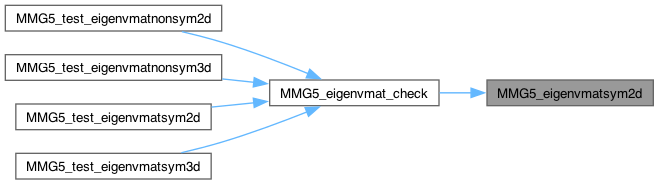
int MMG5_eigenvmatsym3d	(	MMG5_pMesh	mesh,
		double	m[],
		double	lambda[],
		double	v[][3]
	)

Parameters

mesh	pointer to the mesh structure.
m	matrix array.
lambda	eigenvalues array.
v	double array of eigenvectors.

Returns

1 if success, 0 if failure.

Recompose a 3x3 symmetric matrix from its eigenvalue decomposition.

Warning

Eigenvectors in Mmg are stored as matrix rows (the first dimension of the double array spans the number of eigenvectors, the second dimension spans the number of entries of each eigenvector).

Definition at line 164 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_intersecmet22()

int MMG5_intersecmet22	(	MMG5_pMesh	mesh,
		double *	m,
		double *	n,
		double *	mr
	)

Parameters

mesh	pointer to the mesh structure.
m	pointer to a \((2x2)\) metric.
n	pointer to a \((2x2)\) metric.
mr	computed \((2x2)\) metric.

Returns

0 if fail, 1 otherwise.

Compute the intersected (2 x 2) metric from metrics m and n : take simultaneous reduction, and proceed to truncation in sizes.

Definition at line 814 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_intersecmet33()

int MMG5_intersecmet33	(	MMG5_pMesh	mesh,
		double *	m,
		double *	n,
		double *	mr
	)

Parameters

mesh	pointer to the mesh structure.
m	pointer to a \((3x3)\) metric.
n	pointer to a \((3x3)\) metric.
mr	computed \((3x3)\) metric.

Returns

0 if fail, 1 otherwise.

Compute the intersected (3 x 3) metric from metrics m and n : take simultaneous reduction, and proceed to truncation in sizes.

Definition at line 924 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_intmetsavedir()

int MMG5_intmetsavedir	(	MMG5_pMesh	mesh,
		double *	m,
		double *	n,
		double *	mr
	)

Parameters

mesh	pointer to the mesh structure.
m	pointer to the first metric to intersect.
n	pointer to the second metric to intersect.
mr	pointer to the computed intersected metric.

Returns

1.

Compute the intersected (2 x 2) metric between metrics m and n, PRESERVING the directions of m. Result is stored in mr.

Definition at line 635 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_mmgIntextmet()

int MMG5_mmgIntextmet	(	MMG5_pMesh	mesh,
		MMG5_pSol	met,
		MMG5_int	np,
		double	me[6],
		double	n[3]
	)

Parameters

mesh	pointer to the mesh structure.
met	pointer to the metric structure.
np	global index of vertex in which we intersect the metrics.
me	physical metric at point np.
n	normal or tangent at point np.

Returns

0 if fail, 1 otherwise.

Intersect the surface metric held in np (supported in tangent plane of np) with 3*3 physical metric in me. For ridge points, this function fill the \( p_0 \rightarrow m[3]\) and \( p_0 \rightarrow m[4]\) fields that contains respectively the specific sizes in the \(n_1\) and \(n_2\) directions.

Case of a singular point : since MMG5_defmetsin() computes an isotropic metric, scale it by the physical metric while keeping it isotropic

1. Compute minimum size in physical metric. Note that, if we enforce an isotropic metric at singular points, we have 2 direct choices:
   • use the maximal size to make the physical metric iso. In a first guess it seems to be a good idea to limit the impact of singular points over the mesh but in practice it leads to collapse too much. See the following pictures of adaptation over a constant aniso metric with mmgs without gradation and with gradation.
     

     Max siz on sin points, no gradation
     

     Max siz on sin points, with gradation
   • use the minimal size to make the physical metric iso. Adaptation over a constant aniso metric with mmgs without gradation shows the creation of a small element at each corner. The computed iso size correspond to the size imposed on the top surface. With gradation, the gradation removes the anisotropy everywhere so the metric at corners has no effect).
     

     Max siz on sin points, no gradation
     

     Max siz on sin points, with gradation
2. Truncate physical size with respect to mesh constraints
3. Overwrite diagonal metric if physical metric prescribes smaller sizes

Case of a ridge point : take sizes in 3 directions t,n1,u

1. Size prescribed by metric me in direction u1 = n1 ^ t
2. Size prescribed by metric me in direction u2 = n2 ^ t
3. Size prescribed by metric me in direction n1
4. Size prescribed by metric me in direction n2

Case of a ref, or regular point : intersect metrics in tangent plane

1. Expression of both metrics in tangent plane
2. Intersection of metrics in the tangent plane
3. Back to the canonical basis of \mathbb{R}^3 : me = ^tR*mr*R : mtan and metan are reused
4. Truncate the metric in the third direction (because me was not truncated)

Definition at line 1139 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_paratmet()

int MMG5_paratmet	(	double	c0[3],
		double	n0[3],
		double	m[6],
		double	c1[3],
		double	n1[3],
		double	mt[6]
	)

Parameters

c0	table of the coordinates of the starting point.
n0	normal at the starting point.
m	metric to be transported.
c1	table of the coordinates of the ending point.
n1	normal at the ending point.
mt	computed metric.

Returns

0 if fail, 1 otherwise.

Parallel transport of a metric tensor field, attached to point c0, with normal n0, to point c1, with normal n1.

Definition at line 1390 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_sort_eigenv()

void MMG5_sort_eigenv	(	int8_t	dim,
		double *	lambda,
		double *	vp,
		double *	swap,
		int8_t *	perm
	)

Parameters

dim	square matrix size
lambda	eigenvalues array
vp	eigenvectors array
swap	swap array
perm	permutation array

Sort and permute eigenvalues (and eigenvectors) in increasing order.

Definition at line 279 of file mettools.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_test_eigenvmatnonsym2d()

int MMG5_test_eigenvmatnonsym2d	(	MMG5_pMesh	mesh,
		double *	mex,
		double	lambdaex[],
		double	vpex[][2],
		double	ivpex[][2]
	)

Parameters

mesh	pointer to the mesh structure.
mex	test matrix array.
lambdaex	exact eigenvalues array.
vpex	double array of exact right eigenvectors.
ivpex	double array of exact right eigenvectors inverse.

Returns

1 if success, 0 if failure.

For a 2x2 non-symmetric matrix, Test:

• the recomposition of the matrix from its exact eigendecomposition;
• the computation of the eigenvalues of the matrix;
• the computation of the eigenvectors of the matrix;
• the recomposition of the matrix from its numerical eigendecomposition.

Recompose matrix from its eigendecomposition

Compute eigendecomposition

Compute both eigendecomposition and recomposition, and check matrix

Definition at line 379 of file mettools.c.

Here is the call graph for this function:

MMG5_test_eigenvmatnonsym3d()

int MMG5_test_eigenvmatnonsym3d	(	MMG5_pMesh	mesh,
		double *	mex,
		double	lambdaex[],
		double	vpex[][3],
		double	ivpex[][3]
	)

Parameters

mesh	pointer to the mesh structure.
mex	test matrix array.
lambdaex	exact eigenvalues array.
vpex	double array of exact right eigenvectors.
ivpex	double array of exact right eigenvectors inverse.

Returns

1 if success, 0 if failure.

For a 3x3 non-symmetric matrix, Test:

• the recomposition of the matrix from its exact eigendecomposition;
• the computation of the eigenvalues of the matrix;
• the computation of the eigenvectors of the matrix;
• the recomposition of the matrix from its numerical eigendecomposition.

Recompose matrix from its eigendecomposition

Compute eigendecomposition

Compute both eigendecomposition and recomposition, and check matrix

Definition at line 536 of file mettools.c.

Here is the call graph for this function:

MMG5_test_eigenvmatsym2d()

int MMG5_test_eigenvmatsym2d	(	MMG5_pMesh	mesh,
		double *	mex,
		double	lambdaex[],
		double	vpex[][2]
	)

Parameters

mesh	pointer to the mesh structure.
mex	test matrix array.
lambdaex	exact eigenvalues array.
vpex	double array of exact eigenvectors.

Returns

1 if success, 0 if failure.

For a 2x2 symmetric matrix, Test:

• the recomposition of the matrix from its exact eigendecomposition;
• the computation of the eigenvalues of the matrix;
• the computation of the eigenvectors of the matrix;
• the recomposition of the matrix from its numerical eigendecomposition.

Recompose matrix from its eigendecomposition

Compute eigendecomposition

Compute both eigendecomposition and recomposition, and check matrix

Definition at line 301 of file mettools.c.

Here is the call graph for this function:

MMG5_test_eigenvmatsym3d()

int MMG5_test_eigenvmatsym3d	(	MMG5_pMesh	mesh,
		double *	mex,
		double	lambdaex[],
		double	vpex[][3]
	)

Parameters

mesh	pointer to the mesh structure.
mex	test matrix array.
lambdaex	exact eigenvalues array.
vpex	double array of exact eigenvectors.

Returns

1 if success, 0 if failure.

For a 3x3 symmetric matrix, Test:

• the recomposition of the matrix from its exact eigendecomposition;
• the computation of the eigenvalues of the matrix;
• the computation of the eigenvectors of the matrix; the recomposition of the matrix from its numerical eigendecomposition.

Recompose matrix from its eigendecomposition

Compute eigendecomposition

Compute both eigendecomposition and recomposition, and check matrix

Definition at line 456 of file mettools.c.

Here is the call graph for this function:

MMG5_test_intersecmet22()

int MMG5_test_intersecmet22

(

MMG5_pMesh

mesh

)

Parameters

mesh	pointer to the mesh structure.

Returns

0 if fail, 1 otherwise.

Test the intersection of (2 x 2) metrics.

Compute intersection m^{-1}n

Iteratively Recompute intersection of the result with (m,n), changing the matrix to be inverted.

Compute the intersection with n, invert n

Compute the intersection with n, invert intnum

Compute the intersection with n, invert n

Compute the intersection with m, invert intnum

Definition at line 962 of file mettools.c.

Here is the call graph for this function:

MMG5_test_intersecmet33()

int MMG5_test_intersecmet33

(

MMG5_pMesh

mesh

)

Parameters

mesh	pointer to the mesh structure.

Returns

0 if fail, 1 otherwise.

Test the intersection of (3 x 3) metrics.

Compute intersection m^{-1}n

Iteratively Recompute intersection of the result with (m,n), changing the matrix to be inverted.

Compute the intersection with n, invert n

Compute the intersection with n, invert intnum

Compute the intersection with n, invert n

Compute the intersection with m, invert intnum

Definition at line 1047 of file mettools.c.

Here is the call graph for this function: