eigenv.c File Reference

Find eigenvalues and eigenvectors of matrix. More...

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <assert.h>
#include <stdlib.h>
#include <stdint.h>
#include "eigenv_private.h"
#include "mmgcommon_private.h"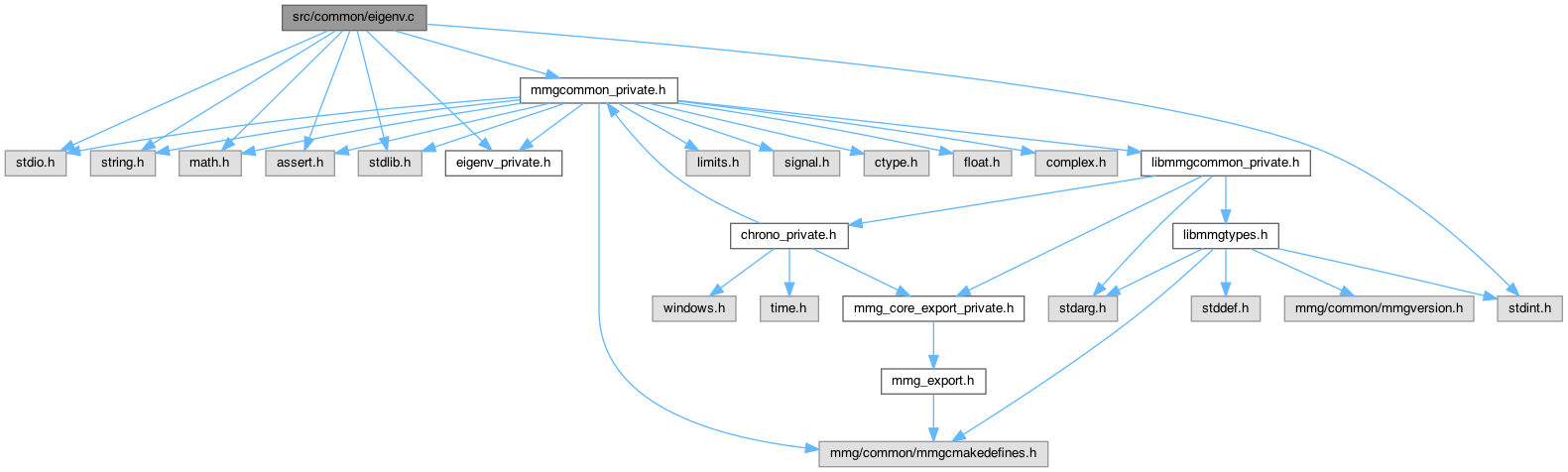

Include dependency graph for eigenv.c:

Go to the source code of this file.

Macros
#define	MG_EIGENV_EPS27   1.e-27
#define	MG_EIGENV_EPS13   1.e-13
#define	MG_EIGENV_EPS10   1.e-10
#define	MG_EIGENV_EPS5e6   5.e-06
#define	MG_EIGENV_EPS6   1.e-06
#define	MG_EIGENV_EPS2e6   2.e-06
#define	MG_EIGENV_EPS5   1.e-05
#define	MAXTOU   50
#define	egal(x, y)

Functions
static int	newton3 (double p[4], double x[3])
	Find root(s) of a polynomial of degree 3.
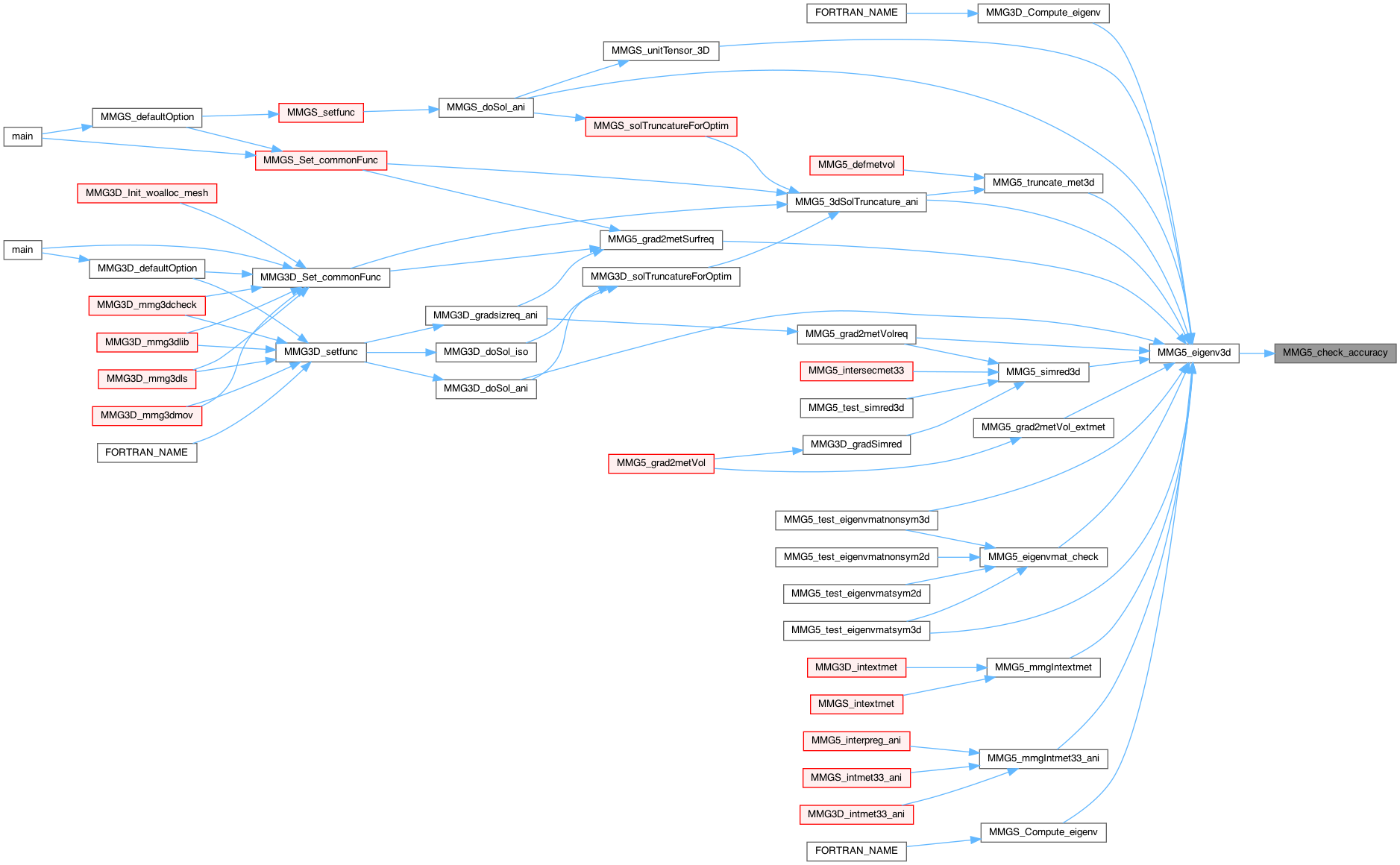
static int	MMG5_check_accuracy (double mat[6], double lambda[3], double v[3][3], double w1[3], double w2[3], double w3[3], double maxm, int order, int symmat)
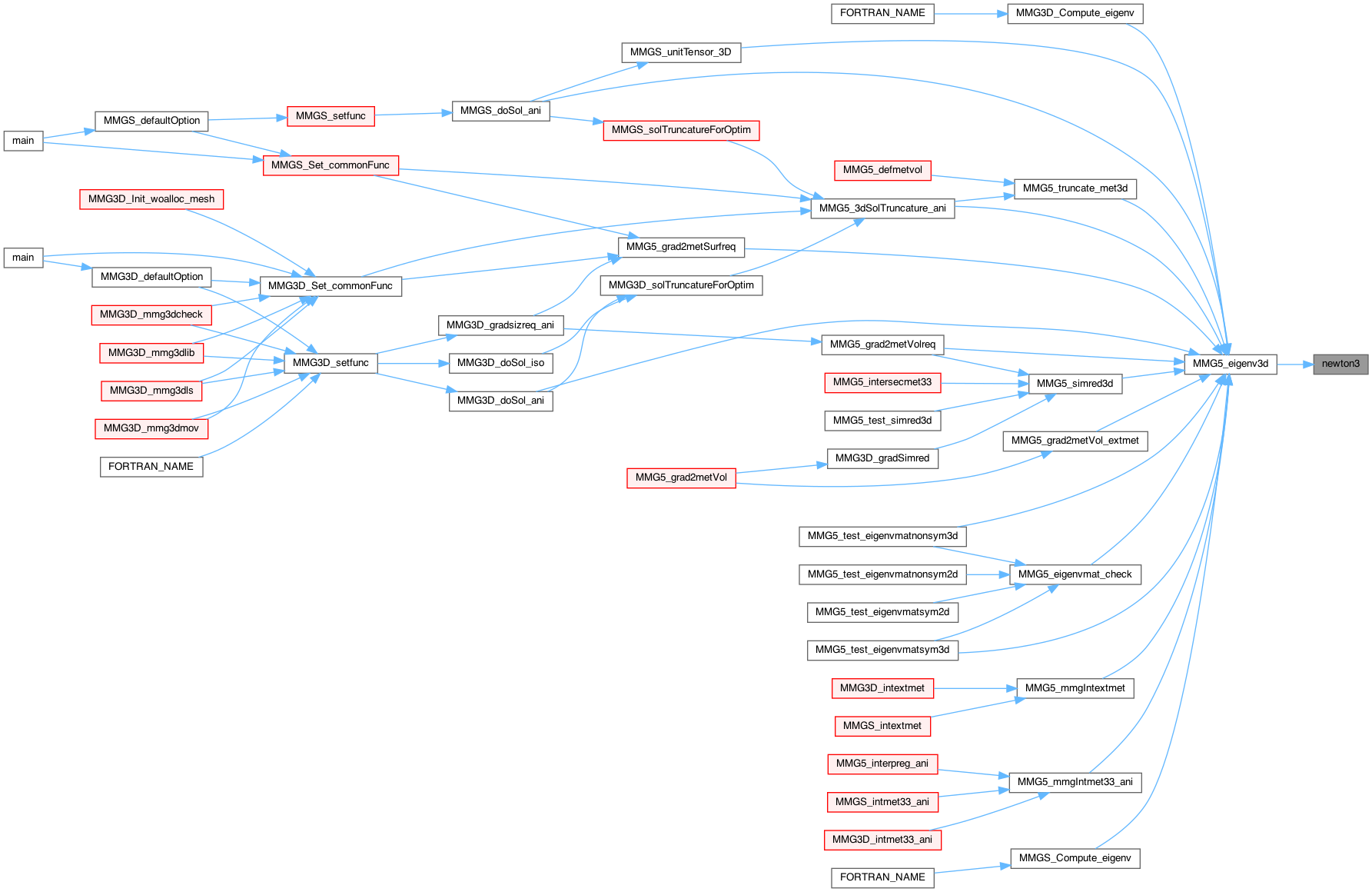
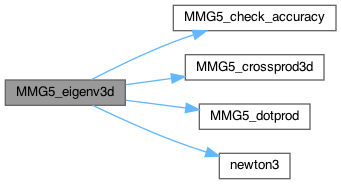
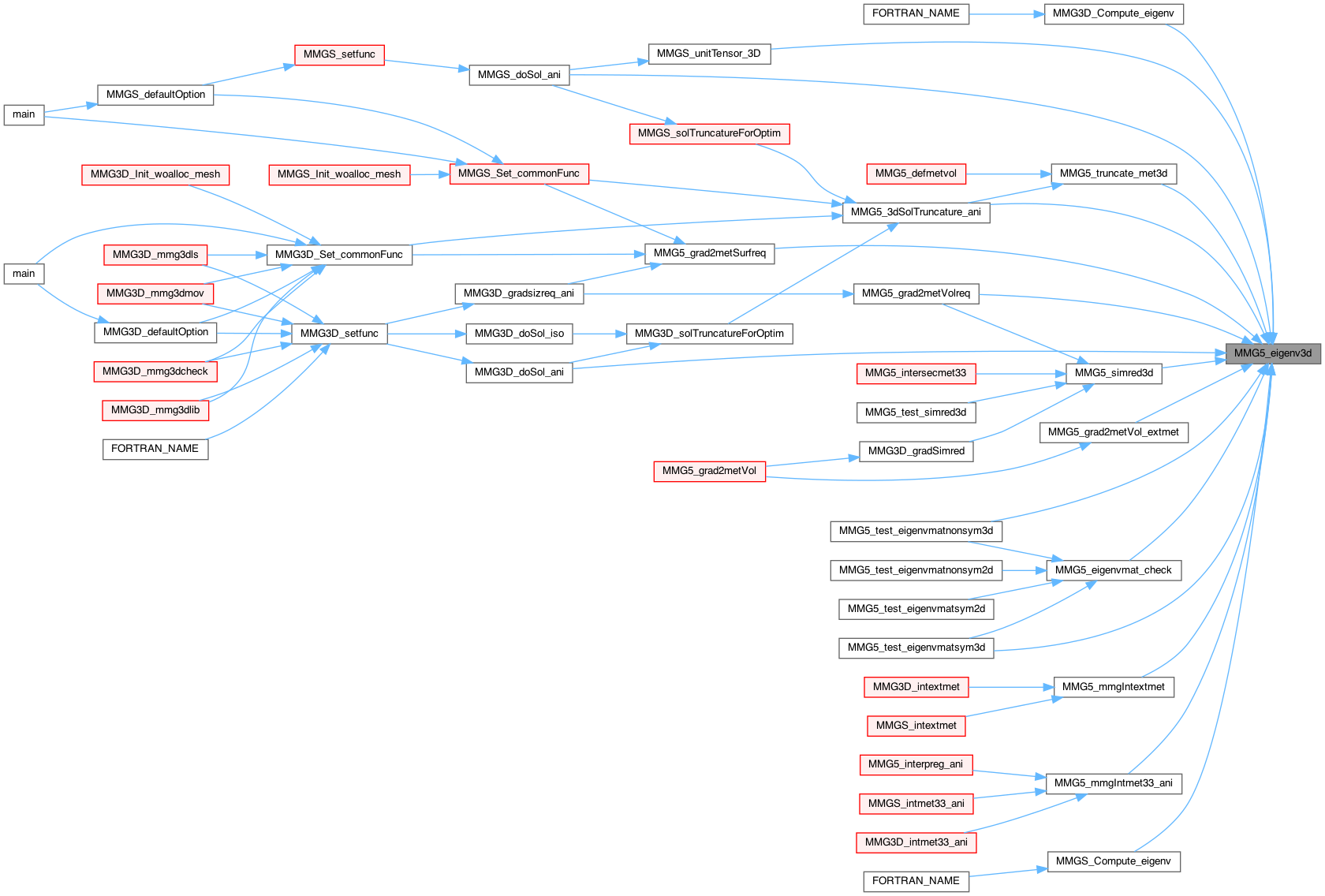
int	MMG5_eigenv3d (int symmat, double *mat, double lambda[3], double v[3][3])
	Find eigenvalues and vectors of a 3x3 matrix.
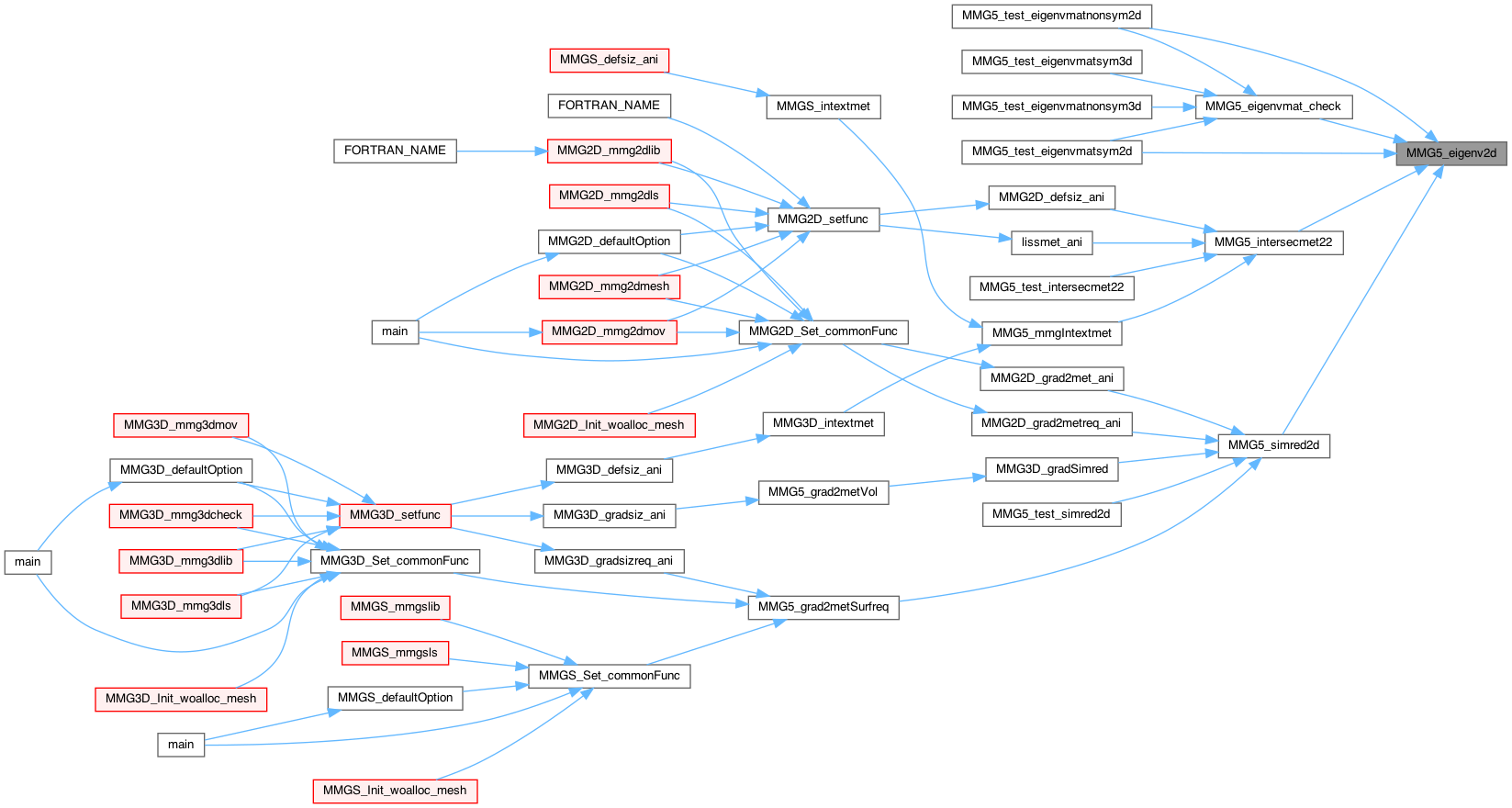
int	MMG5_eigenv2d (int symmat, double *mat, double lambda[2], double vp[2][2])
	Find eigenvalues and vectors of a 2x2 matrix.
int	MMG5_eigen2 (double *mm, double *lambda, double vp[2][2])
	Find eigenvalues and vectors of a 2x2 matrix.
int	MMG5_eigensym (double m[3], double lambda[2], double vp[2][2])

Variables
static double	Id [3][3]
	Identity matrix.

Detailed Description

Find eigenvalues and eigenvectors of matrix.

Author

Cécile Dobrzynski (Bx INP/Inria/UBordeaux)

Pascal Frey (UPMC)

Version

5

Copyright

GNU Lesser General Public License.

Find eigenvalues and eigenvectors of 2x2 or 3x3 symetric definite positive matrix.

Definition in file eigenv.c.

Macro Definition Documentation

egal

#define egal	(		x,
			y
	)

Value:

    (                                             \
    (  ((x) == 0.0f) ? (fabs(y) < MG_EIGENV_EPS6) :                      \
       ( ((y) == 0.0f) ? (fabs(x) < MG_EIGENV_EPS6) :                    \
         (fabs((x)-(y)) / (fabs(x) + fabs(y)) < MG_EIGENV_EPS2e6) )  ) )

Check if numbers x and y are equal.

Definition at line 59 of file eigenv.c.

MAXTOU

#define MAXTOU   50

Definition at line 53 of file eigenv.c.

MG_EIGENV_EPS10

#define MG_EIGENV_EPS10   1.e-10

Definition at line 48 of file eigenv.c.

MG_EIGENV_EPS13

#define MG_EIGENV_EPS13   1.e-13

Definition at line 47 of file eigenv.c.

MG_EIGENV_EPS27

#define MG_EIGENV_EPS27   1.e-27

Definition at line 46 of file eigenv.c.

MG_EIGENV_EPS2e6

#define MG_EIGENV_EPS2e6   2.e-06

Definition at line 51 of file eigenv.c.

MG_EIGENV_EPS5

#define MG_EIGENV_EPS5   1.e-05

Definition at line 52 of file eigenv.c.

MG_EIGENV_EPS5e6

#define MG_EIGENV_EPS5e6   5.e-06

Definition at line 49 of file eigenv.c.

MG_EIGENV_EPS6

#define MG_EIGENV_EPS6   1.e-06

Definition at line 50 of file eigenv.c.

Function Documentation

MMG5_check_accuracy()

static int MMG5_check_accuracy ( double  mat[6], double  lambda[3], double  v[3][3], double  w1[3], double  w2[3], double  w3[3], double  maxm, int  order, int  symmat  )

static

Parameters

mat	pointer to a 3x3 matrix.
lambda	eigenvalues.
v	eigenvectors.
w1	temporary array to perform the matrix cross product.
w2	temporary array to perform the matrix cross product.
w3	temporary array to perform the matrix cross product.
maxm	maximal value of the matrix used for normalization.
order	order of eigenvalues (1,2,3) or 0 if failed.
symmat	0 if matrix is not symetric, 1 otherwise.

Returns

1 if success, 0 if fail.

Check the accuracy of the eigenvalues and vectors computation of a 3x3 matrix (symetric).

Definition at line 311 of file eigenv.c.

Here is the caller graph for this function:

MMG5_eigen2()

int MMG5_eigen2	(	double *	mm,
		double *	lambda,
		double	vp[2][2]
	)

Find eigenvalues and vectors of a 2x2 matrix.

Parameters

mm	pointer to the matrix.
lambda	pointer to the output eigenvalues.
vp	eigenvectors.

Returns

1.

Warning

not used for now

Definition at line 858 of file eigenv.c.

Here is the caller graph for this function:

MMG5_eigensym()

int MMG5_eigensym ( double  m[3], double  lambda[2], double  vp[2][2]  )

inline

Parameters

m	terms of symetric matrix \(2x2\).
lambda	eigenvalues of m.
vp	eigenvectors of m.

Returns

order of the eigenvalues.

Compute eigenelements of a symetric matrix m. Eigenvectors are orthogonal.

Definition at line 973 of file eigenv.c.

Here is the caller graph for this function:

MMG5_eigenv2d()

int MMG5_eigenv2d	(	int	symmat,
		double *	mat,
		double	lambda[2],
		double	vp[2][2]
	)

Find eigenvalues and vectors of a 2x2 matrix.

Parameters

symmat	0 if matrix is not symetric, 1 otherwise.
mat	pointer to the matrix.
lambda	eigenvalues.
v	eigenvectors.

Returns

order of eigenvalues (1,2) or 0 if failed.

Remarks

the i^{th} eigenvector is stored in v[i][.].

Definition at line 780 of file eigenv.c.

Here is the call graph for this function:

Here is the caller graph for this function:

MMG5_eigenv3d()

int MMG5_eigenv3d	(	int	symmat,
		double *	mat,
		double	lambda[3],
		double	v[3][3]
	)

Find eigenvalues and vectors of a 3x3 matrix.

Parameters

symmat	0 if matrix is not symetric, 1 otherwise.
mat	pointer to the matrix.
lambda	eigenvalues.
v	eigenvectors.

Returns

order of eigenvalues (1,2,3) or 0 if failed.

Remarks

the i^{th} eigenvector is stored in v[i][.].

rows of A-lambda[2]*I

rows of A-lambda[0]*I

Definition at line 385 of file eigenv.c.

Here is the call graph for this function:

Here is the caller graph for this function:

newton3()

static int newton3 ( double  p[4], double  x[3]  )

static

Find root(s) of a polynomial of degree 3.

Parameters

p	polynomial coefficients (b=p[2], c=p[1], d=p[0]).
x	root(s) of polynomial.

Returns

0 if no roots.

1 for 3 roots.

2 for 2 roots.

3 for 1 root.

Find root(s) of a polynomial of degree 3: \(P(x) = x^3+bx^2+cx+d\).

Definition at line 86 of file eigenv.c.

Here is the caller graph for this function:

Variable Documentation

Id

double Id[3][3]

static

Initial value:

= {
  {1.0, 0.0, 0.0},
  {0.0, 1.0, 0.0},
  {0.0, 0.0, 1.0} }

Identity matrix.

Definition at line 67 of file eigenv.c.